1. Геометрия
  2. У рівнобічній трапеції ABCD

У рівнобічній трапеції ABCD основа ВС = 4см, висота СЕ = 2√3см, а бічна сторона утворює з основою AD кут 60⁰. Знайдіть діагональ трапеції ​

dikinova2017ozio8q dikinova2017ozio8q    2   22.02.2021 19:52    0

Ответы
JamesBond007007007 JamesBond007007007  24.03.2021 19:53

AC=BD=\sqrt{61} \\S_{ABCD} =7\sqrt{3}

Объяснение:

дано;  ABCD трапеция

BC=4       CE=2√3

∠A = ∠B = 60°

AC=BD= ?   S=?

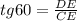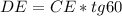
Решение:   из ΔCDE:   tg60=\frac{DE}{CE}  ;         DE = CE* tg60

AE = BC + ED = BC + CE* tg60

AD= DC+2DE=DC+2h*tg60=

AD= DC+2DE=DC+2h*tg60=4+2*2\sqrt{3}*\frac{\sqrt{3} }{2} =4+6=10

из  ΔАСЕ   по т.Пифагора находим  

AC = \sqrt{AE^{2} +CE^{2} } \\AC = \sqrt{(4+2\sqrt{3}*tg60 )^{2} +(2\sqrt{3}) ^{2} } =\sqrt{(4+2\sqrt{3}*\frac{\sqrt{3}}{2} )^{2} +(2\sqrt{3}) ^{2} }

AC=\sqrt{7^{2}+12 }=\sqrt{49+12} = \sqrt{61}

Sтрап = h*(AD+BC)/2

S_{ABCD} = \frac{4+10}{2}*2\sqrt{3}= 7\sqrt{3}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
карим050 карим050  28.05.2019 16:00
Найдите площадь прямоугольной трапеции с основаниями 10 и 18 см и если её большая сторона образует с большим основанием угол 30 градусов....
papulova03 papulova03  28.05.2019 16:00
Найдите площадь параллелограмма, если его высоты равны 10 и 12 см, а острый угол равен 30 градусов....
kjhf2225 kjhf2225  28.05.2019 16:00
Чему равна площадь квадрата? а) произведению катетов на синус угла б) произведению его смежных сторон в) произведению основания на высоту...
ainura8326 ainura8326  28.05.2019 16:00
Чья площадь равна произведению его катетов на синус угла...
WakaAmigo WakaAmigo  28.05.2019 16:00
Втреугольнике авс угол с = 90 градусов. сн высота равна 4. вс корень из 17. найдите тангенса...
Markiza11 Markiza11  28.05.2019 16:00
Втреугольнике abc угол с=90градусов ас=3,tga=корень из 7 деленое на 3. найдите ab...
ismailovu5 ismailovu5  28.05.2019 16:00
Впараллелограмме abcd из вершины тупого угла b провели высоту be к стороне ad ,причем ae=ed найдите площадь параллелограмма abcd если угол a равен 60 градусов,а be=3корень из...
помогите1188 помогите1188  02.07.2019 18:50
Точка м лежит между точками к и р . найдите растояние между м и р, если кр=0,9дм,км =0,3дм...
таня1924 таня1924  27.07.2019 07:30
Дано: треуг. acb - равнобедренный ac - 12 см угол c - 120° сн - биссекриса найти сн-?...
zinovevartem2017 zinovevartem2017  05.12.2020 17:58
Докажите равенство двух треугольников по биссектрисе, углу, из вер- шины которого проведена эта биссектриса, и углу, образованномубиссектрисой со стороной, к которой она проведена.​...

Популярные вопросы