У прямокутнийтрикутник АВС ( В=900) вписано квадрат. Знайдітьплощу квадрата, якщо АВ=12 см, ВС=16 см.
Другие вопросы по теме Геометрия
Популярные вопросы
- ответить на вопросы: № 1. В какой стране родился Фридерик Шопен?...
1 - Какова была задача магистрата?почему выборные должности оставались...
3 - Составьте 1 тонкий и 2 толстых вопроса на тему:как устроен мир...
3 - Какие цели преследовал царизм продвигаясь на территорию Старшего...
1 - Постройте график функции у=2х^2 ; у=1/2 х^2 и опишите свойства...
1 - 2. Отсканируйте QR-код и ознакомьтесь со статьей Дети и интернет:...
2 - Какова сила тяжести плиты массой 2,8 т...
1 - 2. Маса чотирьох апельсин і 2 бананів разом 4,8 кг, а двох апельсин...
3 - вставить пропущенные буквы. Грош вая опера, груш вый нектар, глянц...
1 - очень ОЧЕНЬ ОЧЕНЬ НУЖНО УМОЛЯЮ...
2
Площадь квадрата равна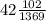 см2.
см2.
Объяснение:
Треугольники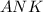 ,
, 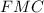 и
и 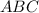 подобны (одинаковые углы обозначены одним цветом).
подобны (одинаковые углы обозначены одним цветом).
Пусть сторона квадрата равна . Тогда из треугольника
. Тогда из треугольника 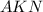
Из треугольника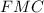
Значит гипотенуза
По теореме Пифагора из треугольника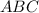
Значит площадь квадрата равна