У коло вписано правильний трикутник периметр 12 см. Найдите периметр квадрата описаного навколо Кола

Ответы

iliabalagansky 11.09.2020 19:46

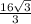
P = $\frac{16\sqrt{3} }{3}$

Объяснение:

1) Оскільки трикутник правильний, то кожна сторона рівна між собою, тобто щоб периметр (сума всіх сторін) був 12, потрібно щоб кожна сторона була по 12/3 = 4 см.

2) Найдемо радіус кола, трикутник якого вписаний в це коло, за формулою для правильного трикутника:

$r = \frac{a\sqrt{3} }{6}$ , де a - сторона трикутника, r - радіус.

Підставимо значення a і отримаємо r:

$r = \frac{4\sqrt{3} }{6} =\frac{2\sqrt{3} }{3}$ .

3) Оскільки квадрат описано навколо того ж самого кола, то всі формули діють і на цей квадрат, і на трикутник одночасно. Формула радіуса кола, описаного навколо квадрата, через радіус вписаного кола звучить так:

$R = r\sqrt{2}$ - Підставимо значення r і отримаємо R:

$R = \frac{2\sqrt{3} }{3} *\sqrt{2} = \frac{2\sqrt{6} }{3}$ - радіус квадрата, описаного навколо кола.

4) Периметр чотирикутника знайдемо за формулою:

$R = \frac{P}{4\sqrt{2} }$ , де P - периметр квадрата. R ми вже знайшли, підставимо значення R і виразимо P:

$\frac{2\sqrt{6} }{3} = \frac{P}{4\sqrt{2} }$ ; $2\sqrt{6} *4\sqrt{2} = 3P$ ; $8\sqrt{12} = 3P$ ; $16\sqrt{3} = 3P$ ; $P = \frac{16\sqrt{3} }{3}$ - периметр квадрата.