У коло радіуса R вписано трапецію, нижня основа якої вдвічі більша від кожної з решти сторін. Знайти площу трапеції.

Площадь трапеции равна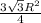

Объяснение:

Пусть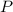 — середина нижнего основания 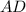. Тогда .

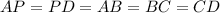Соединим точку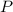 с вершинам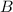и и 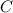. Тогда 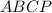и 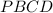ромбы,  а образовавшиеся треугольник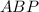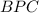и , и 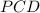— равносторонние.

Из равенства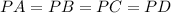 следует, что 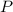— центр описанной окружности, а все перечисленные отрезки — ее радиусы.

Трапеция состоит из трех одинаковых равносторонних треугольников, площадь каждого из которых через сторону вычисляется по формуле

Значит площадь трапеции равна