У ∆АВС відомо, що АС=6 см, ∠А = 80˚, ∠С = 40˚. Знайти радіус кола, описаного навколо трикутника. Я вас очень , объясните как решать НЕ ЧЕРЕЗ ТЕОРЕМУ СИНУСОВ, А ВЫРАЗИТЬ СРАЗУ
Другие вопросы по теме Геометрия
Популярные вопросы
- Словосочетание со словом приморье заранее !...
1 - Решите неравенство содержащие переменную под знаком модуля |2x+3| 9...
1 - Мальчик купил 7 карандашей,а девочка 11 таких же карандашей и заплатила на 12 руб...
1 - 5предложений тұрақты сөз, на казахском языке с переводом на ....
3 - Верно ли выполнено ? 3*9+45=67, 7*9-8=7, (87-39)+(65-28)=85, 51-(27-14)=10 если...
1 - Вслове отварить дверь какой корень зорание...
3 - Найдите предложение, в котором прилагательные употреблены в одной из степеней сравнения....
3 - Слово: новинка-это слово с проверяемой безударной гласной в корне? или с непроверяемой...
2 - Что такое омонимы , они похоже на синонимы ?...
2 - Звукобуквенный анализ слова карандаш...
2
Есть такое свойство в произвольном треугольнике, что точка пересечения серединных перпендикуляров — это центр описанной окружности.
Тоесть, если мы проведём с этого центра отрезок до какой-то вершины треугольника — то этот отрезок будет равен радиусу описанной окружности.
HC == BH == AH = R.
<A = 80°; <AFH == <AEH = 90° ⇒ <FHE = 360-(90+90+80) = 100°.
<FHE = 100° ⇒ <EHC = 180-100 = 80°.
<EHC = 80°; <HEC = 90° ⇒ <HCE = 90-80 = 10°.
AC = 6.
AE == EC = AC/2 ⇒ AE == EC = 6/2 = 3.
EC = 3; <HCE = 10°(α), тоесть — по теореме тангенсов:
Как я говорила, отрезок, проведённый с вершины треугольника до центра описанной окружности — равен радиусу, тоесть: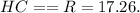
Вывод: R = 17.26.