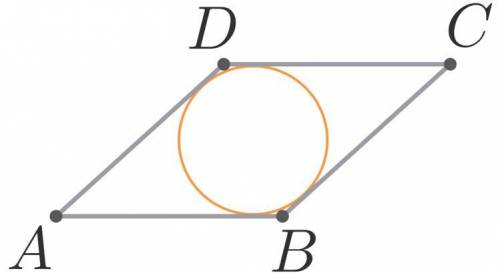
Тупой угол ромба равен 150° Радиус вписанной в этот ромб окружности равен 4 Найдите сторону ромба.

Для решения данной задачи, нам понадобятся знания о свойствах ромба и окружности вписанной в ромб. Давайте разберемся по шагам.

1. В ромбе, все стороны равны друг другу. Обозначим длину стороны ромба как "а".

2. Так как ромб имеет два тупых угла и два острых угла, мы знаем, что сумма углов внутри ромба равна 360 градусов. Из этой информации мы можем сделать вывод о том, что каждый угол ромба равен 360/4 = 90 градусов.

3. В данной задаче у нас есть информация о том, что один из углов ромба является тупым и равен 150 градусов. Так как мы знаем, что все углы внутри ромба равны 90 градусов, мы можем вычислить значение других углов в ромбе. Остальные два угла будут равны по (360 - 150)/2 = 105 градусов каждый.

4. Теперь давайте посмотрим на окружность, вписанную в ромб. Радиус этой окружности равен 4. Зная радиус окружности, мы можем найти диагональ ромба, так как она проходит через центр окружности и имеет длину, равную двум радиусам окружности. Таким образом, диагональ ромба будет равна 2 * 4 = 8.

5. Теперь мы можем разделить диагональ ромба на две части, чтобы найти сторону ромба. При этом одна часть будет равна половине диагонали ромба, а другая часть будет равна стороне ромба. Используя теорему Пифагора в прямоугольном треугольнике, полученном из половины диагонали ромба, диагонали ромба и стороны ромба, мы можем найти значение стороны ромба.

Пошаговое решение:
Диагональ ромба (8) - найдена в шаге 4.
[a] - сторона ромба (что мы хотим найти)

Половина диагонали ромба (4):
(1/2) * 8 = 4

Сторона ромба (а):
Теорема Пифагора: (а^2) = (4^2) + (8^2)
а^2 = 16 + 64
а^2 = 80

а = sqrt(80)
а ≈ 8.944

Ответ: Сторона ромба примерно равна 8.944.