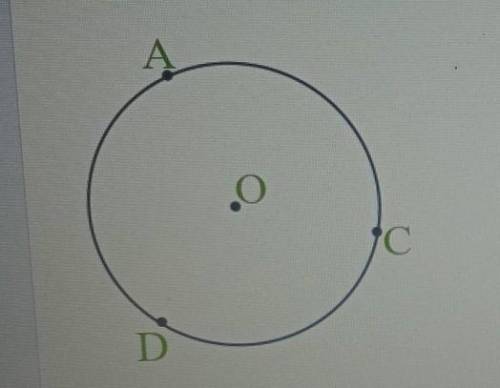
Три точки лежат на окружности с центром О. Найди угол ОСА, если угол АДС равен 73 градуса.​

Для решения данной задачи, нам необходимо использовать свойства окружностей и углы, образованные при пересечении хорд.

1. Первым шагом обратим внимание на то, что точка А находится на окружности с центром О. Следовательно, хорда ОА является радиусом окружности. Так как все радиусы окружности равны между собой, то угол ОАС также является равным 90 градусов.

2. Теперь рассмотрим треугольник ОСА. Угол ОАС равен 90 градусам, а угол АСО -- это искомый угол ОСА.

3. Обратим внимание также на то, что угол АДС равен 73 градусам. Так как хорда АС пересекает радиус ОА, то угол АСО равен половине этого угла, т.е. 73/2 = 36.5 градуса.

4. Поскольку сумма углов треугольника должна быть равна 180 градусам, то для нахождения оставшегося угла ОСА мы можем воспользоваться формулой:
ОСА = 180 - (АСО + ОАС)
ОСА = 180 - (36.5 + 90)
ОСА = 180 - 126.5
ОСА = 53.5 градуса

Таким образом, угол ОСА равен 53.5 градуса.