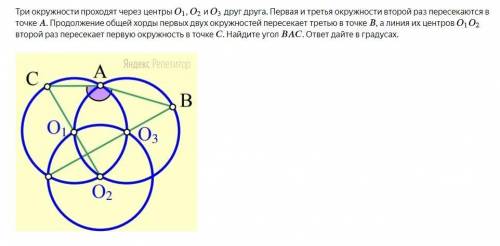
Три окружности проходят через центры , и друг друга. Первая и третья окружности второй раз пересекаются в точке . Продолжение общей хорды первых двух окружностей пересекает третью в точке , а линия их центров второй раз пересекает первую окружность в точке . Найдите угол . ответ дайте в градусах.

∠САВ=165°

Объяснение:

Соединим точки О₁ и А; А и О₃; О₁ и О₃; О₂ и О₃.

Так как три окружности проходят через центры друг друга ⇒их радиусы равны. Пусть радиусы всех окружностей равны R.

1. Рассмотрим Окр. О₁R и Окр. О₂R.

СО₂⊥РО₃ (свойство пересекающихся окружностей)

⇒∠СНВ=90°.

2. Рассмотрим ΔО₁АО₃

О₁А=АО₃=О₃О₁=R

⇒ΔО₁АО₃ - равносторонний.

⇒∠АО₁О₃=60°=∪ АО₃ (центральный)

3. Рассмотрим ΔО₂О₁О₃=равносторонний.

О₁О₃=О₃О₂=О₁О₂=R

⇒∠О₂О₁О₃=60°=∪ О₃О₂ (центральный)

4. ∪ АО₃О₂=∪ АО₃+∪ О₃О₂=60°+60°=120°

5. Рассмотрим Окр. О₁R.

∠О₂СА=120°:2=60° (вписанный)

6. Рассмотрим ΔО₁О₃О₂ равносторонний.

О₃Н⊥РО₃ (п.1)⇒О₃Н-высота, биссектриса (свойство равнобедренного Δ)

⇒∠НО₃О₁=30°=∪ О₁К (центральный)

7. ∠О₁О₃А=60° (ΔО₁АО₃-раввносторонний)

⇒∪ АО₁=∠О₁О₃А=60° (центральный)

8. ∪ КО₁А=∠О₁О₃А+∠КО₃О₁=60°+30°=90°

∠КВА=90°:2=45°(вписанный)

9. Сумма углов четырехугольника равна 360°.

⇒∠САВ=360°-(90°+60°+45°)=165°