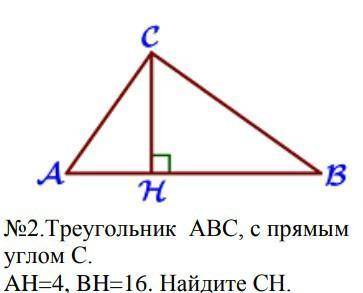
Треугольник АВС, с прямым углом С. AH=4, BH=16. Найдите CH.

Для решения данной задачи мы можем использовать известное соотношение в прямоугольном треугольнике между катетами и гипотенузой. В данном случае, катетами являются отрезки AH и BH, а гипотенузой — отрезок CH.

Известно, что AH = 4 и BH = 16. Мы хотим найти CH.

По теореме Пифагора, в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы:

AH^2 + BH^2 = CH^2

Подставляя значения катетов:

4^2 + 16^2 = CH^2

16 + 256 = CH^2

272 = CH^2

Чтобы найти CH, нам нужно извлечь квадратный корень из обеих сторон, чтобы избавиться от возведения в квадрат:

√(272) = √(CH^2)

Таким образом, CH = √(272).

Для анализа значения √(272) можем использовать калькулятор:

CH ≈ 16.49

Таким образом, длина отрезка CH примерно равна 16.49.