Треугольник АВС правильный,О-центр треугольника ОМ ⊥ АВС,ОМ=2√7. Высота тругольника равна 9. Найдите расстояние от точки Мдо вершин тругольника

8

Объяснение:

по условию треугольник правильный , и О - центр этого треугольника, если ОМ перпендикулярен плоскости треугольника, то точка М равноудалена от вершин ABC

точка О образуется пересечением высот треугольника , она нам дана, и по свойству Высоты , точкой пересечения делятся в отношении 2:1

тогда BO = 2*3=6

отрезок ОМ нам дан, и он ,как сказано в условии, перпендикулярен ABC

Воспользуемся Теоремой Пифагора, и найдём МB

MB=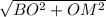 = = 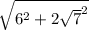= 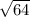8

Тогда MB=MA=MC = 8