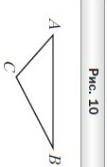
Треугольник ABC является изображением правильного треугольника A1B1C1 (рис. 10). Постройте изображение высоты треугольника, опущенной на сторону A1C1.​

Для построения изображения высоты треугольника, опущенной на сторону A1C1, мы можем воспользоваться следующим алгоритмом:

Шаг 1: Найдем середину стороны A1C1.
- Нарисуем прямую, соединяющую точки A1 и C1. Обозначим ее как l1.
- Возьмем циркуль и, расставив его центр по одну сторону от прямой l1, проведем дугу в районе A1. Обозначим точку пересечения дуги с прямой l1 как D1.
- Проведем другую дугу, используя тот же радиус, но размещая центр по другую сторону от прямой l1. Обозначим точку пересечения этой дуги с прямой l1 как D2.
- Соединим точки D1 и D2 линией, и это будет середина стороны A1C1. Обозначим ее как M.

Шаг 2: Проведем высоту треугольника, опущенную на сторону A1C1.
- Возьмем циркуль, с центром в точке M и радиусом, большим расстояния от M до прямой l1.
- Опустим нижнюю втулку циркуля на точку A1 и проведем дугу, пересекающую прямую A1C1 в точке H1.
- Опустим верхнюю втулку циркуля на точку C1 и проведем другую дугу, пересекающую прямую A1C1 в точке H2.
- Соединим точки H1 и H2 линией, и это будет изображение высоты треугольника, опущенной на сторону A1C1. Обозначим его как h.

Теперь нарисуем получившуюся фигуру.

Мы должны иметь на рисунке:
- Изображение треугольника ABC и треугольника A1B1C1.
- Прямую l1, соединяющую точки A1 и C1.
- Середину стороны A1C1, обозначенную как M.
- Высоту треугольника, опущенную на сторону A1C1, обозначенную как h, проходящую через точки H1 и H2.

Теперь приступим к деталям алгоритма и построению фигуры:

Шаг 1:
1.1. Нарисуйте прямую, соединяющую точки A1 и C1.
1.2. Положите циркуль на точку A1 и происходя из нее проведите дугу, пересекающую прямую A1C1. Обозначим точку пересечения дуги с прямой A1C1 как D1.
1.3. Положите циркуль на точку C1 и происходя из нее проведите дугу, пересекающую прямую A1C1. Обозначим точку пересечения дуги с прямой A1C1 как D2.
1.4. Соедините точки D1 и D2 прямой линией. Обозначим получившуюся прямую как l2.

Шаг 2:
2.1. Поставьте циркуль на точку M и нарисуйте дугу, пересекающую прямую l2. Обозначим точку пересечения дуги с прямой l2 как H1.
2.2. Поставьте циркуль на точку M и нарисуйте другую дугу, пересекающую прямую l2. Обозначим точку пересечения дуги с прямой l2 как H2.
2.3. Соедините точки H1 и H2 прямой линией. Обозначим получившуюся прямую как h.

Теперь у нас есть изображение высоты треугольника, опущенной на сторону A1C1.

Хочу отметить, что ответ будет понятен школьнику при условии, что он знаком с терминами "середина стороны" и "высота треугольника". Если он не знаком с этими понятиями, можно предварительно объяснить их значения и примеры их применения.