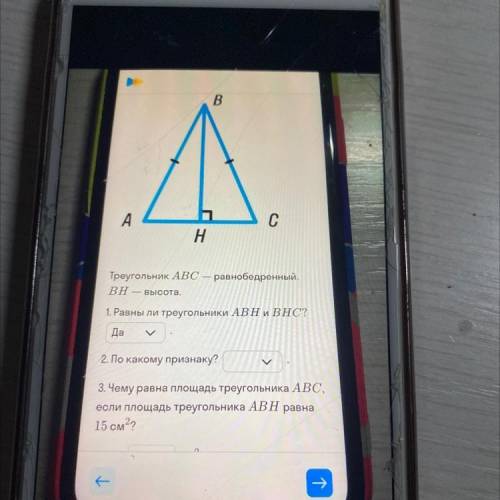
Треугольник ABC — равнобедренный. BH — высота.
1. Равны ли треугольники ABH и ВНС?
Да
2. По какому признаку?
3. Чему равна площадь треугольника ABC,
если площадь треугольника ABH равна
15 см2?
ответ:
см2.

1. Чтобы определить, равны ли треугольники ABH и ВНС, нужно проверить, выполняется ли условие равенства двух сторон и углов треугольников. В данном случае можно заметить, что сторона AB равна стороне BC (так как треугольник ABC является равнобедренным) и угол ABH равен углу BCH (так как BH - это высота, перпендикулярная основанию треугольника). Поэтому можно сказать, что треугольники ABH и ВНС равны.

2. Признаком равенства треугольников является равенство двух сторон и углов. В данном случае стороны AB и BC равны, а углы ABH и BCH равны, поэтому треугольники ABH и ВНС равны по признаку "равенство двух сторон и углов".

3. Чтобы найти площадь треугольника ABC, нужно использовать формулу площади треугольника, которая составляет половину произведения длины основания треугольника на длину высоты, опущенной на это основание. В данном случае, основание треугольника ABC это сторона BC, а высота треугольника это отрезок BH.

Так как площадь треугольника ABH равна 15 см2, мы можем использовать эту информацию для решения. По формуле площади треугольника ABH:

Площадь ABH = (1/2) * BC * BH = 15

В данной формуле BC это основание треугольника ABH, а BH это высота. По условию мы знаем, что BC равно 10 см, поэтому можем подставить это значение и уравнение примет вид:

(1/2) * 10 * BH = 15

Умножим 10 на BH и получим:

5 * BH = 15

Теперь разделим обе части на 5:

BH = 3

Таким образом, длина высоты BH равна 3 см.

Теперь мы можем найти площадь треугольника ABC, используя эту информацию. По формуле площади треугольника ABC:

Площадь ABC = (1/2) * BC * BH

Подставим значения:

Площадь ABC = (1/2) * 10 * 3 = 15 см2

Ответ: Площадь треугольника ABC равна 15 см2.