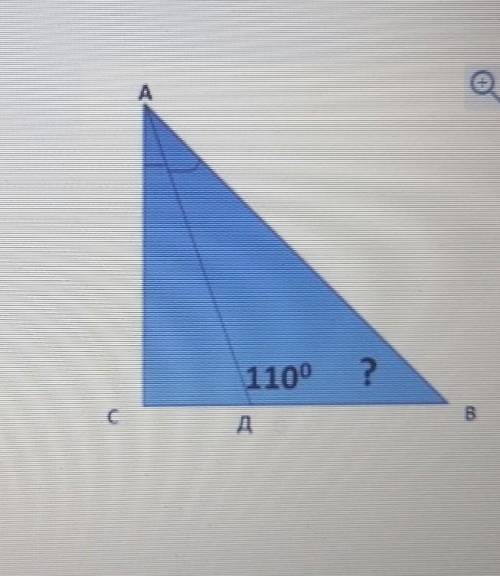
Треугольник ABC прямоугольный. По данным чертежа найдите угол B. Варианты ответов:
1) 70
2) 50
3) 40
Другие вопросы по теме Геометрия
Популярные вопросы
- На проводник длиной 0,5 м, расположенный под углом 30° к вектору магнитной индукции,...
3 - На проводящих горизонтальных параллельных направляющих лежат два металлических...
2 - Заряженная частица движется в однородном магнитном поле с постоянной по модулю...
2 - На прямолинейный проводник длиной 50 см действует сила Ампера, равная 0,25 Н....
2 - Как проверить предположение о природе взаимодействия кольца с магнитом, используя...
1 - В треугольнике АВС, АВ=12, ВС=9.Отрезок MN параллелен ВС, причем точка М лежит...
1 - В каком случае сила Лоренца, действующая на движущуюся заряженную частицу в магнитном...
2 - Квадратная проволочная рамка перпендикулярна вектору магнитной индукции однородного...
3 - В однородном магнитном поле по окружности радиусом 5 см движется протон- Чему...
1 - На протон, влетевший в однородное магнитное поле со скоростью 3*10^6 м/с, направленной...
3
1. Сначала вспомним теорему Пифагора, которая гласит: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
В нашем случае, катеты это отрезки AB и BC, а гипотенуза - отрезок AC. То есть, AC^2 = AB^2 + BC^2.
2. Подставим известные значения в это уравнение. Исходя из чертежа, длина AB равна 6, а длина BC равна 8.
Таким образом, AC^2 = 6^2 + 8^2 = 36 + 64 = 100.
3. Чтобы найти длину AC, возьмем квадратный корень из 100: AC = √100 = 10.
4. Теперь у нас есть стороны треугольника. Для нахождения угла B можно использовать соотношение тангента:
tg(B) = противолежащий катет / прилежащий катет.
В данном случае, мы хотим найти tg(B), где противолежащий катет - AB, а прилежащий катет - BC.
5. Подставим известные значения и найдем tg(B):
tg(B) = AB / BC = 6 / 8 = 0.75.
6. Чтобы найти угол B, мы можем использовать тангенс в обратном направлении, получив арктангенс. То есть,
B = arctg(0.75).
7. Используя калькулятор, найдем арктангенс от 0.75: B ≈ 36.87°.
Таким образом, угол B приближенно равен 36.87°. По вопросу, предложенному варианту ответа, ближайший вариант из списка - 40° (ответ 3).