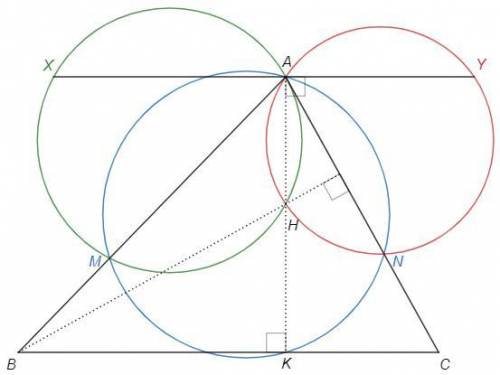
Треугольник ABC, AK - высота, H - ортоцентр. Окружность, проходящая через точки A и K, пересекает AB и AC в точках M и N соответственно. Через точку A проходит прямая, параллельная BC. Окружности AHM и AHN пересекают эту прямую в точках X и Y соответственно. Докажите, что XY=BC.

Пусть точка, в которой BC пересекает синюю окружность второй раз это K1. На приложенном к условию чертеже она немного левее точки K. Эта окружность проходит через точки A и K, а точка K1 может быть в произвольном месте, но её положение полностью определяет саму окружность.

Поскольку ∠K1KA = 90°; => K1A - диаметр синей окружности.

По этой же причине

∠K1NA = 90°; ∠K1MA = 90°

Поэтому K1M и K1N - перпендикулярны AB и AC, соответственно.  

Прежде, чем решать саму задачу, см. рисунки 1 и 2, приложенные к решению. На них решается вс задача, нечто вроде леммы. Я сохранил обозначения, но важно! - что точка H там НЕ является ортоцентром - это произвольная точка на AK. Эта "лемма" доказана там для двух вариантов местоположения точки K1, когда точка H находится внутри отрезка AK. Интересующиеся могут попробовать исследовать другие варианты.

На третьем прилагаемом рисунке - чертеж для решения самой задачи.

Первый шаг - строится окружность по трем точкам A H M и еще одна - на BK1, как на диаметре, эта окружность пройдет через точку M, так как ∠K1MB = 90°. Точка P - это вторая точка пересечения этих окружностей (она есть обязательно, так как уже есть одна - точка M). Второй шаг - по доказанной лемме K1X проходит через точку P и перпендикулярно BH, которая тоже проходит через точку P.

И третье - теперь (вот только теперь!) надо вспомнить, что H - точка пересечения высот (ортоцентр) треугольника ABC, то есть XK1 II AC  - обе прямые перпендикулярны BH; => K1XAC - параллелограмм, => XA = K1C;

Доказательство того, что BK1 = AY, аналогичное. => XY = BC; чтд.

Но есть еще более интересная штука. Треугольник K1XY вообще оказывается ЦС-отражением треугольника ABC относительно середины AK1 - центра синей окружности. Интересно, а нет ли тут какой-то гомотетии?