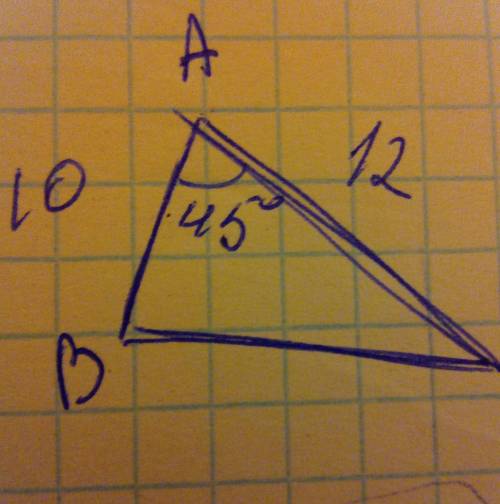
Треугольник ABC,AB=10,AC=12.Угол А=45
Найти: S ABC​

Для решения этой задачи, нам сначала необходимо найти длину третьей стороны треугольника, а затем применить формулу для вычисления площади треугольника.

Для нахождения длины стороны BC, мы можем использовать теорему косинусов. Формула теоремы косинусов выглядит следующим образом:
c^2 = a^2 + b^2 - 2ab*cos(C),
где c - длина стороны C, a и b - длины других двух сторон треугольника, C - между ними угол.

В нашем случае, a = AB = 10, b = AC = 12, C = угол BAC = 45 градусов.
Подставляем значения в формулу:
BC^2 = 10^2 + 12^2 - 2 * 10 * 12 * cos(45).

Далее, мы можем вычислить длину стороны BC, возведя обе части уравнения в квадрат и извлекая квадратный корень:
BC = √(10^2 + 12^2 - 2 * 10 * 12 * cos(45)).

Теперь, когда у нас есть длины всех трех сторон треугольника, мы можем применить формулу Герона для вычисления площади треугольника. Формула Герона выглядит следующим образом:
S = √(p * (p - a) * (p - b) * (p - c)),
где S - площадь треугольника, a, b, c - длины сторон треугольника, p - полупериметр.

Для нашего треугольника, a = 10, b = 12, c = BC (которую мы только что нашли), и полупериметр p можно вычислить, сложив длины всех трех сторон, и разделив на 2:
p = (10 + 12 + BC) / 2.

Подставляем значения в формулу:
S = √(((10 + 12 + BC) / 2) * (((10 + 12 + BC) / 2) - 10) * (((10 + 12 + BC) / 2) - 12) * (((10 + 12 + BC) / 2) - BC)).

Теперь остается только вычислить это выражение и получить результат.

Надеюсь, данное объяснение помогло вам понять, как решить данную задачу. Если возникнут еще вопросы, не стесняйтесь задавать их.