Трапейсия и окружность, вписанная как то не так

2

Объяснение:

Найдем сначала x. Пусть окружность касается AB и BC в точках K и L соответственно. Тогда BK=BL=x. Аналогично CL=x. Тогда BC=2x => x=1. Радиус, проведенный в точку касания, перпендикулярен к касательной. Тогда, если O - центр окружности, OK=OL=R и OK⊥AB, а OL⊥BC. Значит ∠KBL+∠KOL=180°. Тогда по теореме косинусов для четырехугольника KBLO можно выразить KL² двумя через OK=OL=R и BK=BL=1. Приравняем KL². Получим: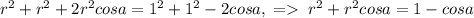 . Здесь cosa - косинус ∠KBL. 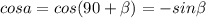, где 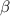- угол ABH. AB=10x=10, а AH=(14-2)/2=6 => 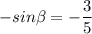. Подставим это: .

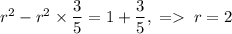Задание выполнено!