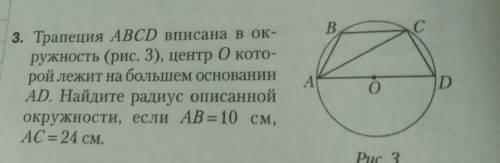
трапеция ABCD вписан в окружность центр о которой лежит на большем основании AD найдите радиус описанной окружности если ab 10 см а сколько есть. ​

Для начала, давайте разберемся с основными свойствами вписанных многоугольников. Вписанный многоугольник – это многоугольник, все вершины которого лежат на окружности. Одно из основных свойств вписанных многоугольников гласит, что угол, образованный любыми двумя сторонами такого многоугольника, равен половине центрального угла, опирающегося на ту же самую дугу окружности.

В нашем случае мы имеем трапецию ABCD, где окружность вписана внутри трапеции. По условию, центр окружности лежит на большем основании AD. Обозначим центр окружности как O.

Чтобы найти радиус описанной окружности, нам необходимо определить длину отрезка OD (радиус окружности).

Для начала, рассмотрим треугольник AOB. Он является равнобедренным, поскольку стороны AO и BO равны ( радиусы окружности равны) и, следовательно, угол AOB равен 30 градусам (половина центрального угла, опирающегося на дугу AB).

Также, рассмотрим треугольник BOD. Он является равнобедренным, так как стороны BO и BD равны (радиусы окружности равны). Поскольку мы уже определили угол AOB как 30 градусов, то угол BOD также будет равен 30 градусам.

Зная угол BOD, мы можем определить угол ODA. Радиус AO является высотой треугольника AOD, а сторона AD – основанием. По свойству равнобедренных треугольников, высота, опущенная из вершины острого угла, делит основание пополам. Таким образом, угол ODA тоже равен 30 градусам.

Теперь, зная угол ODA, мы можем определить угол OAD. Угол OAD также равен 30 градусам, так как треугольник OAD является равнобедренным (радиусы OA и OD равны).

Таким образом, мы определили все углы в треугольнике OAD, и он является равносторонним. Значит, все его стороны равны. Радиус OD равен стороне AD и половине длины стороны AB.

По условию, сторона AB равна 10 см. Отсюда следует, что сторона AD равна 20 см (AB = 2*AD).

Таким образом, радиус описанной окружности (OD) также равен 20 см.

Итак, радиус описанной окружности равен 20 см.