1. Геометрия
  2. Трапеция ABCD, основание BC которой

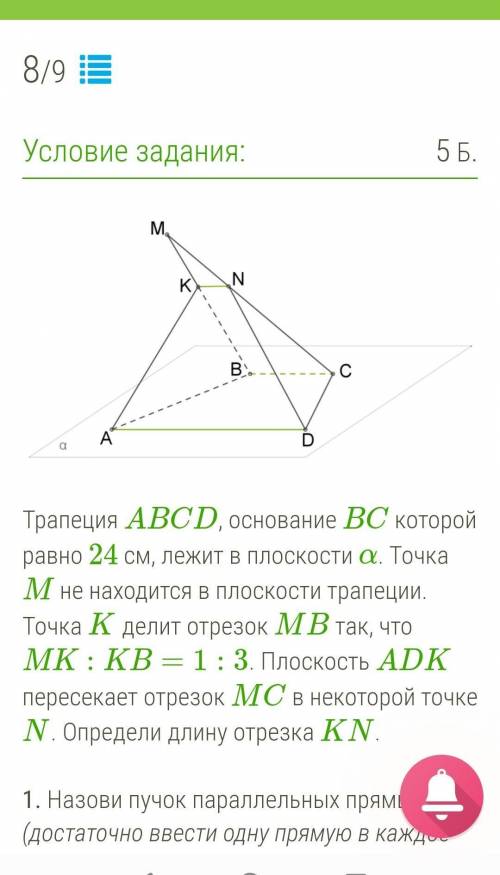
Трапеция ABCD, основание BC которой равно 24 cм, лежит в плоскости α. Точка M не находится в плоскости трапеции. Точка K делит отрезок MB так, что MK:KB=1:3. Плоскость ADK пересекает отрезок MC в некоторой точке N. Определи длину отрезка KN. 1. Назови пучок параллельных прямых (достаточно ввести одну прямую в каждое окошко, буквы располагай в алфавитном порядке!):

∥
∥
.
2. Назови подобные треугольники:
ΔKMN~Δ
.

3. KN=
(округли до одной десятой).
Предыдущее задание
Предыдущее задание
Список заданий
Список заданий
Следующее задание
Следующее задание
​


Трапеция ABCD, основание BC которой равно 24 cм, лежит в плоскости α. Точка M не находится в плоскос

ilyagnomm ilyagnomm    2   31.12.2020 07:57    161

Ответы
nadiakrasavtze nadiakrasavtze  12.02.2021 21:43

1) AD∥BC∥KN

 

AD∥BC как основания трапеции, значит BC∥(ADK).

Если плоскость (BCK) проходит через прямую BC, параллельную плоскости (ADK), и пересекает эту плоскость по прямой KN, тоKN∥BC.

 

2) Треугольники BMC и KMN подобны и BCKN=BMKM

 

3) KN=BC⋅KMBM=BC⋅KMBK+MK=12⋅1(1+4)=2,4

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Сакура2034 Сакура2034  01.04.2019 05:10
На сторонах мк и кр треугольника мкр выбраны точки а и в так, что угол мра равен углу арм. отрезки мв и ра пересекаются в точке о, причём ов=оа. докажите, что треугольник мкр -...
Dashylik228 Dashylik228  01.04.2019 05:10
Длина окружности основания цилиндра 24 п. наибольшее расстояние между точками верхнего и нижнего основания цилиндра 30. вычислите объем цилиндра...
Дисконет Дисконет  17.07.2019 13:00
Решите ! продолжения боковых сторон трапеции авсд,пересекаются в точке о.найдите во и отношение площадей треугольников вос и аод, ад=5см,вс=2см,ао=25см.можно с рисунком)...
GordienkoA20 GordienkoA20  17.07.2019 13:00
Вравнобедренном треугольнике угол при вершине равен 70 градусов. вычислите градусную меру угла между основанием и высотой проведенная к боковой стороне...
Darklife1 Darklife1  17.07.2019 13:00
Вокружности с центром о отрезки ac и bd-диаметры. центральный угол aod=116. найдите вписанный угол acb...
Marina20151111 Marina20151111  17.07.2019 13:00
Найти сумму корней (в градусах) уравнения 2sin^2 2x +(1- корень из 3)sin4x-2 корня из 3 cos^2 2x =0 на отрезке [0; 225]...
лооол19 лооол19  09.07.2019 00:30
Abcd- трапеция, верхнее основание =5см, а нижнее основание = 12см. найти периметр трапеции , если в ее можно вписать окружность....
s1138285 s1138285  09.07.2019 00:30
Через середину отрезка ab проведена прямая перпендикулярная прямой ab докажите что каждая точка x этой прямой одинаково удалена от точки а и б...
SarJiG2A SarJiG2A  04.09.2019 15:50
Для четырёхугольника abcd запишите: 1)вершины, соседние с вершиной а; 2)вершину противолежащую вершине в; 3) стороны соседние со стороной cd 4)сторону противолежащую стороне bc;...
dbonapik dbonapik  04.09.2019 15:50
Один из острых углов прямоугольного треугольника abc = 60 градусов, а сумма короткого катета и гипотенузы 24 см. определите длину короткого катета....

Популярные вопросы