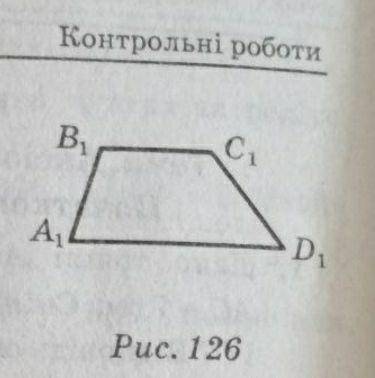
Трапеция A1B1C1D1 - изображение трапеции ABCD, в которой AB=CD=AD DC меньше AD. Постройте изображение центра круга, которое прикасается к боковым сторонам и большей основе трапеции ABCD

Другие вопросы по теме Геометрия
Популярные вопросы
- Решите уравнение: 1. х (в квадрате) = 64 ; 2.(х-2) ( в квадрате) = 25...
3 - Саэродрома вылетел вертолет со скоростью 210 км/ч. через 2 часа с этого же...
3 - Твір на тему моя улюблена рослина...
2 - Напишите формулу алканы, в состав которого входят 24 атома водорода. вычислите...
2 - Постройте словообразовательные цепочки, показывая последовательность образования...
2 - За 6 авторучек миша заплатил 42 рубля. сколько таких авторучек он сможеть...
3 - Найти художественные средства выразительности фет а. а. - «бабочка» ты прав....
1 - Скласти розповідь на тему кормушка для птахів...
3 - Жель у рыб вырабатывается: а)поджелудочной железой б)желудком в) печнью г)в...
3 - Слушайте как там будет an yacht или a yacht просто лень лезть в правило (:...
1
Построим перпендикуляры к боковым сторонам трапеции ABCD. Пусть M1 и N1 - середины сторон A1B1 и C1D1 соответственно.
Для начала найдем длину сторон A1M1 и B1N1:
Мы знаем, что AB = CD = AD. Также, поскольку трапеция ABCD является изображением трапеции A1B1C1D1, то AB || A1B1 и CD || C1D1. Значит, по теореме Пифагора, получим:
AM1 = √(AD^2 - DM1^2)
BM1 = √(AD^2 - DM1^2)
Для определения DM1 воспользуемся теоремой Фалеса:
DM1 / BM1 = CD / AB = DC / AD
Так как CD = DC и AD > DC, получим:
DM1 / BM1 = CD / AB = 1/2
Отсюда можно выразить DM1:
DM1 = BM1 / 2
Теперь мы можем найти длины сторон A1M1 и B1N1:
AM1 = √(AD^2 - (BM1 / 2)^2)
BM1 = √(AD^2 - (BM1 / 2)^2)
Теперь построим перпендикуляры из точек M1 и N1 на стороны AB и CD соответственно:
Пусть P1 и Q1 - точки на стороне AB, такие что P1M1 и Q1N1 перпендикулярны AB.
Теперь мы можем найти длину стороны A1P1 и B1Q1:
AP1 = AM1 - MP1
В предыдущем шаге мы нашли AM1, а MP1 является половиной BM1, значит:
AP1 = AM1 - MP1 = √(AD^2 - (BM1 / 2)^2) - BM1 / 2
BQ1 = BN1 - N1Q1
Аналогично, BN1 и N1Q1 найдутся из данных в предыдущем шаге.
Мы нашли длины сторон A1P1 и B1Q1. Теперь проведем отрезки P1Q1 и найдем его середину - это будет центр круга, который мы ищем.
Построение всех отрезков и нахождение середины P1Q1 может быть выполнено с помощью линейки и циркуля.