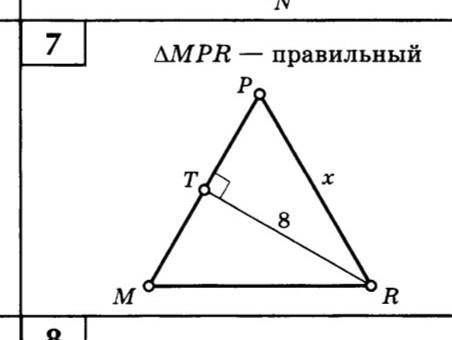
Tr=8
угол T= 90°
найти: PR

Для решения данной задачи, нам понадобится использовать теорему Пифагора и тригонометрические соотношения. Итак, давайте начнем: 1. Известно, что угол T равен 90 градусов, значит треугольник PTR является прямоугольным (угол T - прямой угол). 2. Из теоремы Пифагора следует, что квадрат гипотенузы (отрезка PR) равен сумме квадратов катетов: PR^2 = PT^2 + TR^2 3. Подставим известные значения в формулу: PR^2 = PT^2 + TR^2 PR^2 = 8^2 + TR^2 PR^2 = 64 + TR^2 4. В задаче не указана длина отрезка PT (катета), поэтому нам нужно его найти. Для этого воспользуемся тригонометрическим соотношением для прямоугольного треугольника: тангенс угла T (тангенс 90 градусов) равен отношению противолежащего катета (PT) к прилежащему катету (TR): тангенс T = PT / TR В данной задаче тангенс 90 градусов бесконечно велик (неопределенность), что значит PT = некоторое конечное число, TR = 0 и PT^2 = 0. Теперь мы можем заменить PT^2 в формуле для PR^2 (шаг 3): PR^2 = 64 + TR^2 PR^2 = 64 + 0 PR^2 = 64 5. Теперь проведем корень из обеих частей уравнения, чтобы найти значение PR: PR = √(64) PR = 8 Ответ: Длина отрезка PR равна 8 единицам длины.