тому, кто решит эту задачу про треугольник и окружность!
2 часа уже не могу решить.

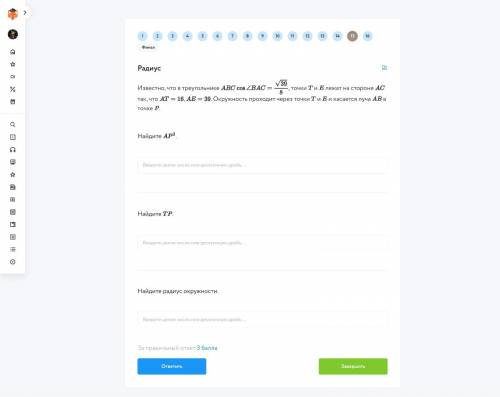
Решение основано на свойстве угла между секущей и касательной, который равен половине центрального угла в точки касания и пересечения.

Треугольник АРT получается равнобедренным, отсюда определяется первая искомая величина: РТ = 16.

АР = 2*16*cos A = 2*16*(√39/8) = 4√39 ≈ 24,98.

Вторая искомая величина: АР² = 16*39 = 624.

Находим косинус двойного угла:

cos(2A) = 2cos²A - 1 = (2*39/64) - 1 = 14/64 = 7/32.

По теореме косинусов в треугольнике РОТ находим:

(r² + r² - 16²)/(2*r*r) = 7/32.

Отсюда находим r = 12,8.