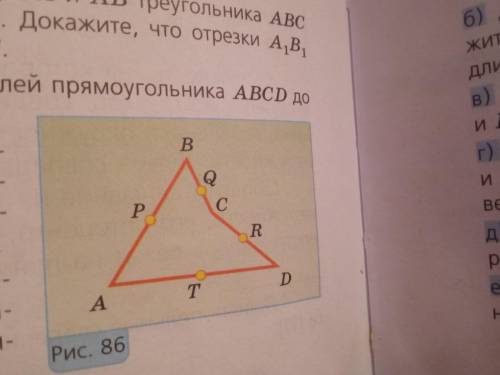
Точки P, Q, R и T на рисунке 86 — середины сторон четырехугольника ABCD. Докажите, что четырехугольник PQRT — параллелограмм.
Другие вопросы по теме Геометрия
Популярные вопросы
- Охарактеризуйте период стабилизации в сша в 20-годах. какие факторы обусловили...
3 - Что можно увидеть на городской площади...
3 - Сообщение на тему: биография к. линнея в кратце. желательно с планом...
1 - 30% от 50 35% от 12,6 42% от 5/7 65% от 5 1/13...
3 - Всего 2 вопроса! 1)электролитической диссоциацией называется процесс распада:...
2 - Принадлежность покрытосеменных растений к тому или иному семейству определяться...
1 - Шёл а с сумкой за плечом.вижу, бьёт в овраге ключ. наклонившись над ключом, уронил...
1 - 10 предложений с одушевленными существительными из разных рассказов...
2 - Напишите все даты и определения эпохи петра первого!...
2 - На першому сеансі в кінотеатрі було 47 глядачів. на другому-у 7 разів більше...
1
Для доказательства, что четырехугольник PQRT является параллелограммом, мы должны показать, что его противоположные стороны параллельны.
Первым шагом мы можем заметить, что точки P и Q являются серединами сторон AB и BC соответственно. Значит, отрезок PQ будет средней линией треугольника ABC. Такой отрезок параллелен и равен половине стороны треугольника. Точно так же, точки R и T являются серединами сторон CD и DA, поэтому отрезок RT также будет средней линией треугольника CDA.
Зная это, мы можем заметить, что отрезки PQ и RT являются параллельными и равными, так как они являются средними линиями треугольников ABC и CDA соответственно.
Далее, нам остается доказать, что отрезки TP и QR параллельны. Для этого мы можем воспользоваться свойством параллельных прямых, которое гласит: если две прямые параллельны, то у них углы попарно равны.
Давайте рассмотрим углы A и C и треугольники ABC и CDA. Так как отрезки PQ и RT параллельны сторонам AB и CD, то мы можем сделать следующее предположение: угол A равен углу C, так как это углы при параллельных сторонах. Таким же образом, получаем, что угол C равен углу A.
Из этого следует, что отрезки QR и TP являются параллельными, так как они лежат на противоположных сторонах отрезков PQ и RT и их углы попарно равны.
Таким образом, мы доказали, что противоположные стороны четырехугольника PQRT, то есть отрезки PQ и RT, а также отрезки QR и TP, параллельны. По определению параллелограмма, PQRT является параллелограммом.
Надеюсь, это объяснение было понятным и убедительным. Если у вас остались вопросы, пожалуйста, задавайте!