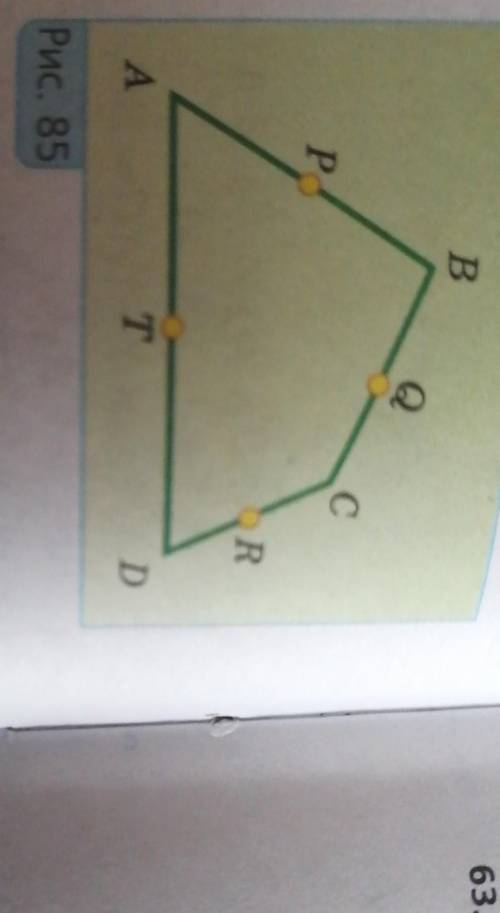
Точки P, Q, R и T на рисунке 85 — середины сторон четырехугольника ABCD. Докажите, что четырехугольник PQRT — параллелограмм.​

Добрый день! Для доказательства того, что четырехугольник PQRT является параллелограммом, нам необходимо использовать свойства серединных перпендикуляров и свойства параллелограмма.

Давайте разберемся подробнее. По условию, точки P, Q, R и T являются серединами сторон четырехугольника ABCD. Для начала, давайте обозначим точку M, которая является серединой стороны AB, и точку N, которая является серединой стороны BC.

Согласно свойству серединных перпендикуляров, мы можем сказать, что MN перпендикулярна стороне AC, так как MN является серединным перпендикуляром к отрезку AC. Аналогично, мы можем сказать, что PT параллельна стороне AC, так как PT является серединным перпендикуляром к отрезку AC.

Теперь давайте рассмотрим стороны AB и CD. Так как P и Q являются серединами этих сторон, то по аналогии с предыдущим рассуждением мы можем сказать, что PQ параллельна стороне AB. Аналогично, мы можем сказать, что RT параллельна стороне CD.

Итак, мы показали, что PT и PQ параллельны стороне AC, а RT и PQ параллельны стороне CD. Следовательно, все стороны четырехугольника PQRT параллельны попарно.

Также, мы можем заметить, что сторона PT равна стороне RQ (так как они являются серединными перпендикулярами), и сторона PQ равна стороне TR (так как они являются серединными перпендикулярами). Это свойство параллелограмма - противоположные стороны равны и параллельны.

Итак, мы доказали, что все стороны четырехугольника PQRT параллельны попарно и противоположные стороны равны. Следовательно, четырехугольник PQRT является параллелограммом.

Я надеюсь, что объяснение было понятным и полезным для тебя! Если у тебя возникнут еще вопросы, не стесняйся задавать их. Я всегда готов помочь!