Точки P и Q — середины рёбер AD и CC1 куба ABCDA1B1C1D1 соответственно. Ребро куба равно 3. пункт а) решила
б) Найдите расстояние между прямыми B1P и BQ
ответ должен получиться: 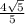
!

Другие вопросы по теме Геометрия
Популярные вопросы
- Постройте отрицательные и вопросительные предложения (альтернативный, разделительный,...
1 - Как правильно написать отросль или отрасль? это слово исключение. и надо написать...
3 - Масса котенка 3/5 кг а масса щенка 1 целая 3/4 кг. какими будут показания весов...
1 - Назовите грамматическое значение, которые следующими окончаниями. примеры слов...
3 - Помгите решить 9 класс по теме использование систем уравнений с двумя переменными...
1 - Вычислите площадь фигуры, ограниченной линиями у = 1 – х3, у = 0, х = -1...
3 - Вставьте глагол to be или to have got в present, past или future. 1. he a pupil...
2 - Записать слова в форме предложного падежа: мозоль, печаль,король, тюль, огонь,...
1 - Буду ! 1) is anything wrong? no. think) the party tonight. 2) these days )-)...
2 - 1)один из острых углов прямоугольного треугольника равен 60 градусов.разность...
3
Объяснение:
а) Проведем РК║АВ.
РК⊥(ВВ₁С₁), значит В₁К - проекция прямой В₁Р на плоскость (ВВ₁С₁).
ΔВ₁ВК = ΔBCQ по двум катетам, значит
∠1 = ∠2 и ∠3 = ∠4.
∠1 + ∠3 = 90°, значит в ΔКВМ ∠1 + ∠4 = 90°, следовательно,
∠ВМК = 90°, т.е. В₁К⊥BQ.
Но тогда и B₁P⊥BQ по теореме о трех перпендикулярах.
б)
РК⊥(ВВ₁С₁), значит РК⊥BQ,
BQ⊥B₁K (доказано в п. а), тогда BQ⊥(В₁КР).
Проведем МН⊥В₁Р в треугольнике В₁КР.
Так как МН⊂(В₁КР), то МН⊥BQ и МН⊥В₁Р по построению, тогда
МН - искомое расстояние между прямыми B₁P и BQ.
На выносном рисунке:
ΔВСQ = ΔEC₁Q по катету и острому углу (CQ = C₁Q и углы при вершине Q равны как вертикальные), ⇒ ЕС₁ = ВС = 3.
ΔВ₁МЕ ~ ΔKMB по двум углам (при вершине М - вертикальные и ∠1 = ∠Е как накрест лежащие при ВС║В₁Е и секущей ВЕ):
Из прямоугольного треугольника В₁ВК по теореме Пифагора:
Из прямоугольного треугольника В₁КР по теореме Пифагора:
ΔB₁MH: