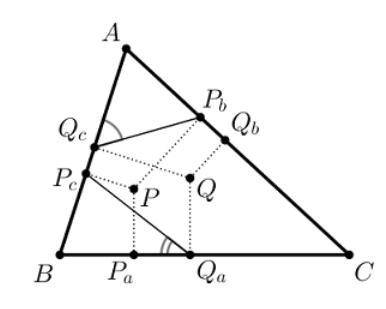
Точки P и Q изогонально сопряжены относительно треугольника ABC. Обозначим через Pa, Pb и Pc проекции точки P на стороны BC, CA и AB соответственно, а через Qa, Qb и Qc — проекции точки Q на стороны BC, CA и AB соответственно. Известно, что ∠PbQcA=53∘, ∠PcQaB=36∘. Найдите ∠PaQbC.
Другие вопросы по теме Геометрия
Популярные вопросы
- 4.На каких традициях был воспитан герой повести С.Жунусова «Прозрение»?ребят...
2 - Составьте биографическую справку на одного из лидеров партии Алаш...
3 - 1-Какое кравооброщение безпазвоночных животных? 2-какая симетрия скелета...
3 - СОЧ Размер вируса гриппа равен 0.000 000 103 м. Запись этого числа в...
2 - Вооб...и, раз...езд, пер...я, раз...военный, об...явление,...
2 - Три причины долголетия Византии, наследницы Восточной Римской империи...
3 - Составьте характеристику героя (как зовут героя, чем он занимается, его...
1 - На рисунке показан график, описывающий движение автомобиля: a) вычислите...
2 - 1You watch TV at night. 2You drop litter in the street. 3You drink milk...
1 - 3. Прочитайте информацию и дайте ответы на вопросы: a) В 568 году согдийский...
1
Мы знаем, что ∠PbQcA = 53∘. Следовательно, угол PbQ также равен 53∘.
Также, мы знаем, что ∠PcQaB = 36∘. Следовательно, угол QcB равен 36∘.
Теперь обратимся к треугольнику ABC и рассмотрим вершину B. Рассмотрим угол QbC. Учитывая, что Qb является проекцией точки Q на сторону AC, и учитывая свойство изогональной сопряженности, можно сделать вывод, что угол QbC равен углу QcA.
Но мы уже знаем, что угол QcA равен углу PbQ, который равен 53∘. Следовательно, ∠QbC = 53∘.
Из прямой суммы углов треугольника мы можем найти угол ∠PaQbC. Угол ∠PaQbC равен сумме углов QbC и PbQ.
∠PaQbC = ∠QbC + ∠PbQ
∠PaQbC = 53∘ + 53∘
∠PaQbC = 106∘
Таким образом, угол ∠PaQbC равен 106∘.