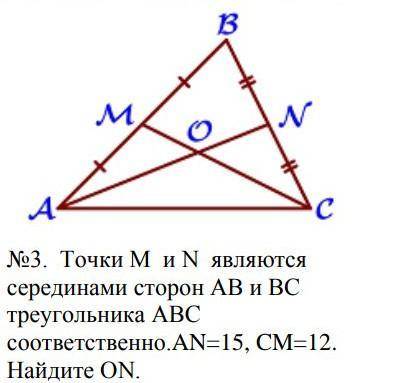
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно.AN=15, CM=12. Найдите ON

Чтобы найти длину отрезка ON, мы должны воспользоваться свойством серединного перпендикуляра. Согласно этому свойству, серединный перпендикуляр делит сторону треугольника пополам и является перпендикуляром к этой стороне.

В данном случае, точка M является серединой стороны AB, поэтому отрезок MN делит сторону AB пополам и является перпендикуляром к AB. Аналогично, точка N является серединой стороны BC, поэтому отрезок MN делит сторону BC пополам и является перпендикуляром к BC.

Теперь мы можем воспользоваться свойством прямоугольного треугольника, чтобы найти длину отрезка ON. В треугольнике ONM, ON является гипотенузой, а MN является одним из катетов.

Мы можем использовать теорему Пифагора, которая гласит: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Таким образом, мы можем записать:

ON^2 = OM^2 + MN^2

Так как точка M является серединой стороны AB, значит, отрезок AM равен отрезку MB. Дано, что AN = 15, значит, AM также равно 15. Таким образом, мы можем записать:

OM = AM - AO

OM = 15 - ON (по определению серединного перпендикуляра)

Теперь мы можем подставить это выражение в наше уравнение:

ON^2 = (15 - ON)^2 + MN^2

Раскроем скобки:

ON^2 = 225 - 30ON + ON^2 + MN^2

Теперь упростим уравнение:

0 = 225 - 30ON + MN^2

Перенесем все члены к одной стороне:

30ON = 225 + MN^2

ON = (225 + MN^2) / 30

Таким образом, чтобы найти длину отрезка ON, нам нужно знать значение длины отрезка MN. Если значение длины отрезка MN дано, то мы можем подставить его в формулу и рассчитать длину отрезка ON.