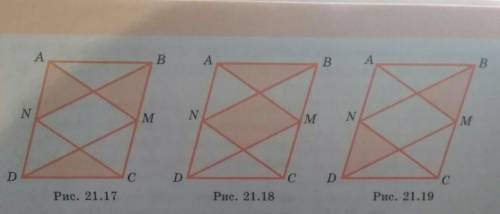
Точки М и N - середины сторон BC и AD середины сторон BC и AD параллелограмма ABCD
(рис. 21.17, 21.18, 21.19). Чему равна сумма площадей закрашенных частей параллелограмма, если площадь параллелограмма ABCD
равна 56?
нужно решение на рисунок 21.18. и 21.19.​

Добрый день! Давайте разберемся, как решить эту задачу.

Сначала давайте определим, какие формулы нам понадобятся. Мы знаем, что площадь параллелограмма равна произведению длины одной из сторон на высоту, опущенную на эту сторону. Также нам понадобится формула для площади треугольника – половина произведения длины основания на соответствующую высоту.

На рисунке 21.18 мы видим, что точка М – середина стороны BC, а N – середина стороны AD. Что это значит? Это значит, что точка М делит сторону BC на две равные части, а точка N делит сторону AD на две равные части.

Мы можем использовать эти сведения, чтобы разбить параллелограмм на два треугольника и прямоугольник.

Рассмотрим треугольник MBN. Его площадь равна половине произведения длины основания BN на соответствующую высоту – высоту, опущенную из точки M. Так как BN – это половина основания BC, то длина основания BN равна BC/2. Возьмем в качестве высоты высоту, опущенную из точки M. Понятно, что эта высота равна высоте всего параллелограмма (ведь так как М – середина стороны BC, то высота, опущенная из точки M, равна высоте, опущенной из точки B). Поэтому площадь треугольника MBN равна 0.5 * (BC/2) * высота всего параллелограмма. Вспомним, что площадь параллелограмма равна 56, и обозначим высоту всего параллелограмма буквой h. Получим следующее уравнение: 0.5 * (BC/2) * h = 56.

Аналогично, рассмотрим треугольник MAD. Его площадь равна половине произведения длины основания AD на высоту, опущенную из точки M. Длина основания AD равна BC/2 (так как точка N делила сторону AD на две равные части), а высота всего параллелограмма равна h. Поэтому площадь треугольника MAD равна 0.5 * (BC/2) * h.

Таким образом, сумма площадей треугольников MBN и MAD равна 0.5 * (BC/2) * h + 0.5 * (BC/2) * h = (BC/2) * h.

На рисунке 21.19 мы видим, что у нас имеется еще один прямоугольник, нашей задачей является определить его площадь.

Обратим внимание, что идентичные треугольники MBN и MAD также делят на две равные части диагонали AC и BD соответственно. Это значит, что точки M и N также делят диагонали на две равные части.

Получаем, что поразмерно прямоугольник, закрашенный нами, есть прямоугольник АМCB, причем этот прямоугольник имеет стороны, равные половине соответствующих сторон параллелограмма, то есть, его длина AM равна BC/2, а его ширина MC равна AD/2.

Теперь мы можем найти площадь прямоугольника АМCB. Эта площадь равна произведению длины одной из сторон на другую сторону, то есть (BC/2) * (AD/2).

Наконец, сумма площадей треугольников MBN и MAD, а также площади прямоугольника АМCB равна (BC/2) * h + (BC/2) * h + (BC/2) * (AD/2).

Нам известно, что площадь параллелограмма равна 56, поэтому можем записать следующее уравнение: (BC/2) * h + (BC/2) * h + (BC/2) * (AD/2) = 56.

Это уравнение содержит две неизвестные: BC/2 и AD/2, поэтому нам нужно еще дополнительное условие, чтобы решить задачу окончательно. Если вы можете предоставить дополнительную информацию или уточнения, я с радостью помогу вам решить эту задачу еще более детально.