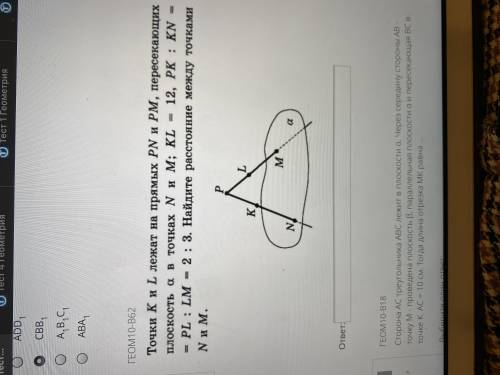
Точки K и L лежат на прямых pn и pm, пересекающих плоскость а в точках N и M; KL=12,PK:KN=PL:LM=2:3. Найдите расстояние между точками N и M
Другие вопросы по теме Геометрия
Популярные вопросы
- При каком значении c график функции y = 5(x + 2)2 + 6x + 4c проходит...
2 - Задание Какую ценную информацию можно взять из данногоисточника?Бехистунская...
2 - 5. I... (switch) on the computer and ... (open) the document....
3 - Первое, сделать рисунки и обозначить все, поставить знаки, заранее...
1 - Сравните географическое положение природные условия и ресурсы...
3 - 1 Полумай и ответь каким образом уйгуры расширяли земельные наделы...
2 - 1 Chips go for / with everything, don t they? 2 nll pay for /...
3 - Используя текст параграфа 35-35 стр 131-134. запиши причины переселения...
2 - Напишите сказку для первоклассников на тему Как растут деревья...
1 - Сколько будет sin 10°10 ? ...
2
Из условия задачи мы имеем следующую информацию:
1. Длина отрезка KL равна 12.
2. Отношение длин PK:KN равно 2:3.
3. Отношение длин PL:LM равно 2:3.
Предлагаю решить эту задачу по шагам:
Шаг 1: Обозначим неизвестное расстояние между точками N и M как x.
Шаг 2: Используя отношение длин PK:KN = 2:3, разделим отрезок KN на 5 равных частей: KN1 и N1N2.
Пусть KN1 = 2a, тогда N1N2 = 3a.
Шаг 3: Аналогично, используя отношение длин PL:LM = 2:3, разделим отрезок LM на 5 равных частей: LM1 и M1M2.
Пусть LM1 = 2b, тогда M1M2 = 3b.
Шаг 4: Так как N1N2 и M1M2 являются соответствующими сторонами подобных треугольников KNN1 и LMM1, то отношение длин этих отрезков будет также равно 2:3.
Шаг 5: Теперь у нас есть следующие равенства:
N1N2 = 3a и M1M2 = 3b
Также KL = KN1 + N1N2 + M1M2 + LM1, поэтому
12 = 2a + 3a + 3b + 2b
12 = 5a + 5b
12 = 5(a + b)
Шаг 6: Решим полученное уравнение относительно суммы a + b:
12 = 5(a + b)
12/5 = a + b
Шаг 7: Заметим, что a + b = N1N2 + M1M2 = N2M2, поэтому сумма a + b представляет расстояние между точками N и M.
Шаг 8: Подставим значения, которые мы получили ранее:
a + b = 12/5
Таким образом, расстояние между точками N и M составляет 12/5 или 2.4.