Точки f, o и t - соответственно середины ребер bc, dc и ac тетраэдра dabc. периметр треугольника fot равен 12 см. вычислите площадь боковой поверхности тетраэдра.

Тетраэдр это многоугольник состоящий из 4 граней, для решения задачи необходимо, чтобы все его рёбра были равны или какое-то ещё дополнительное условие, иначе для решения задачи не хватает данных.

F, O, T - середины ребер BC, DC, AC соответственно. Поэтому FO, OT, TF - средние линии треугольников CBD, CDA, CAB соответственно. А значит, BD=2FO, DA=2OT, AB=2TF.

BD+DA+AB = 2FO+2OT+2TF = 2(FO+OT+TF) = 2·12см = 24см.

ΔBDA - равносторонний (все рёбра тетраэдра равны), поэтому BD=DA=AB=24см:3=8см. Найдём площадь равностороннего треугольника по формуле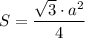 , где a - сторона треугольника.

см².

Площадью боковой поверхности, будет площадь любых 3 граней (все грани это равные, равносторонние треугольники).

S(бок.) =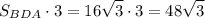 см².

ответ: 48√3 см².