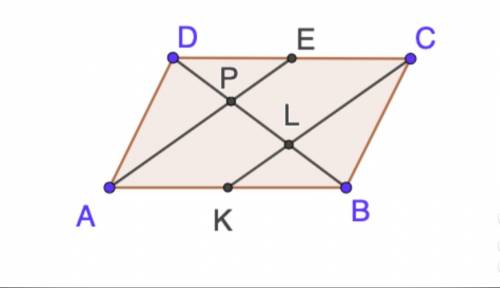
Точки E и K – середины сторон CD и AB параллелограмма ABCD, отрезки AE и CK пересекают диагональ в точке BD
Найдите отношение BL : LP : PD

АВ=CD так как противоположные стороны параллелограмма равны. Тогда 0,5*АВ=0,5*CD.

Так как К – середина АВ, то АК=0,5*АВ.

Так как Е – середина CD, то ЕС=0,5*CD.

Получим что АК=ЕС.

АК//ЕС, так как AB//CD, поскольку противоположные стороны параллелограмма параллельны.

Тогда получим что AECK – параллелограмм, так как противоположные стороны паралельны и равны. Следовательно АЕ//КС так как противоположные стороны параллелограмма параллельны.

По обобщённой теореме Фалеса: параллельные прямые отсекают на сторонах угла пропорциональные отрезки.

То есть:

Пусть СЕ=n, тогда ED=n так же, так как CE=ED. Тогда:

Пусть AK=m, тогда КВ=m так же, так как AK=KB.

Получим что PD:LP:BL=1:1:1, или иначе говоря отрезки равны.

ответ: 1