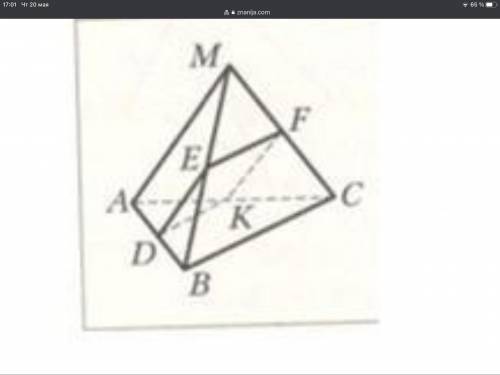
Точки D, E, F и K средины рёбер AB, MB, MC, AC тетраэдра MABC соответственно BC = 42 СМ, AM = 36см. Докажите, что точки D, E, F, K являются вершинами параллелограмма, и вычеслите периметр этого параллелограмма
Другие вопросы по теме Геометрия
Популярные вопросы
- Маша написала на доске все числа от 1 до 1000. сколько цифр она при...
1 - Составь звуковые модели выделенных слов. подъезд - зв., -б., -сл....
1 - Сколько кг содержится в : 1\4т,3\4т,3\10т,13\10т...
3 - Какого происхождения ископаемые в кольско-карельской и двинско-печерской...
2 - Сделать письменно-буквенный разбор слова зимой...
3 - :** о люцерне серповидной- листья: тип прикрепления на стебель: травянистый...
2 - Ночь. темно. за стеной шумит метель. в маленькой комнате перед иконой...
3 - Придумать предложение на со словом ,,survey ,переводится ,как исследование,обзор,опрос...
1 - При каком значении x выражение |2x-3|+6 принимает наименьшее значение?...
3 - Таблица истинности не могу понять как решать.....
1
Точки D, E, F и K средины рёбер AB, MB, MC, AC тетраэдра MABC соответственно BC = 42 СМ, AM = 36см. Докажите, что точки D, E, F, K являются вершинами параллелограмма, и вычислите периметр этого параллелограмма.
Объяснение:
1) DE-средняя линия ΔАВМ ⇒ DE=1/2*36=18(см) и DE║АМ;
KF-средняя линия ΔАМC ⇒ KF=1/2*36=18(см) и KF║АМ.
По признаку параллелограмма о равных и параллельных сторонах четырехугольника, DEFK-параллелограмм.
2) Р=2*(DE+DK).
DК-средняя линия ΔАВС ⇒ DК=1/2*42=21(см) .
Р=2*(18+21)=78( см) .