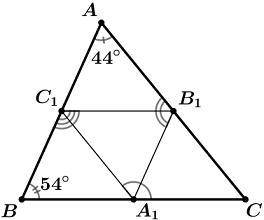
Точки A1, B1 и C1 — середины сторон BC, CA и AB треугольника ABC. Известно, что ∠A=44∘, ∠B=54∘. Найдите сумму ∠C1A1C+∠A1B1A+∠B1C1B.

можно без решения

Для решения данной задачи, нам понадобится использовать свойства углов треугольника.

Из условия задачи мы знаем, что точки A1, B1 и C1 - это середины сторон BC, CA и AB соответственно. Перейдем к обозначениям углов треугольника ABC:
∠A - угол при вершине A,
∠B - угол при вершине B,
∠C - угол при вершине C.

Также мы знаем, что ∠A = 44∘ и ∠B = 54∘.

Для нахождения суммы ∠C1A1C + ∠A1B1A + ∠B1C1B, мы можем использовать следующие свойства:

1. Сумма углов треугольника равна 180∘. Мы можем использовать эту информацию для нахождения третьего угла треугольника ∠C:
∠C = 180∘ - ∠A - ∠B
∠C = 180∘ - 44∘ - 54∘
∠C = 82∘

2. Среди треугольников, образованных вершинами и серединами сторон треугольника ABC, существует строгая пропорциональность углов. Это означает, что соответствующие углы между сторонами одного из вспомогательных треугольников будут равны соответствующим углам треугольника ABC.

Теперь, чтобы найти сумму ∠C1A1C + ∠A1B1A + ∠B1C1B, мы можем рассмотреть треугольники ∆C1A1C, ∆A1B1A и ∆B1C1B.

1. Треугольник ∆C1A1C: в этом треугольнике угол при вершине A1 является соответствующим углом ∠C треугольника ABC, поэтому ∠C1A1C = ∠C = 82∘.

2. Треугольник ∆A1B1A: в этом треугольнике угол при вершине B1 является соответствующим углом ∠A треугольника ABC, поэтому ∠A1B1A = ∠A = 44∘.

3. Треугольник ∆B1C1B: в этом треугольнике угол при вершине C1 является соответствующим углом ∠B треугольника ABC, поэтому ∠B1C1B = ∠B = 54∘.

Таким образом, сумма ∠C1A1C + ∠A1B1A + ∠B1C1B равна:

∠C1A1C + ∠A1B1A + ∠B1C1B = ∠C + ∠A + ∠B
= 82∘ + 44∘ + 54∘
= 180∘

Ответ: Сумма ∠C1A1C + ∠A1B1A + ∠B1C1B равна 180∘.