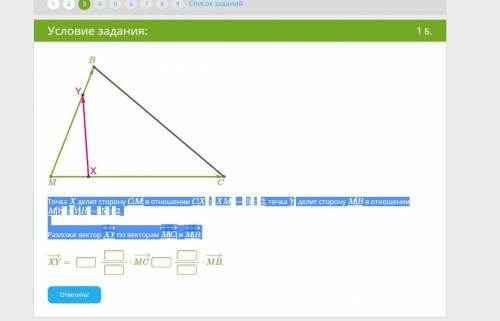
Точка X делит сторону CM в отношении CX:XM=5:2, точка Y делит сторону MB в отношении MY:YB=5:2.

Разложи вектор XY−→ по векторам MC−→− и MB−→−:

Для того чтобы разложить вектор XY по векторам MC и MB, мы должны сначала найти векторы MC и MB.

Из условия "Точка X делит сторону CM в отношении CX:XM=5:2", мы можем выразить вектор MC через вектор CX и вектор XM. Поскольку отношение CX:XM равно 5:2, мы можем представить вектор MC как сумму векторов CX и XM, умноженных соответственно на 5/7 и 2/7:

MC = (5/7) * CX + (2/7) * XM

Аналогичным образом, из условия "Точка Y делит сторону MB в отношении MY:YB=5:2", мы можем представить вектор MB как сумму векторов MY и YB, умноженных соответственно на 5/7 и 2/7:

MB = (5/7) * MY + (2/7) * YB

Теперь мы можем разложить вектор XY по векторам MC и MB. Для этого нам нужно найти коэффициенты a и b, такие чтобы:

XY = a * MC + b * MB

Подставим значения MC и MB, которые мы нашли ранее:

XY = a * [(5/7) * CX + (2/7) * XM] + b * [(5/7) * MY + (2/7) * YB]

Раскроем скобки:

XY = (5/7) * [a * CX + b * MY] + (2/7) * [a * XM + b * YB]

Теперь нам нужно найти значения a и b. Мы можем представить вектор XY как линейную комбинацию векторов CX, MY, XM и YB. Поскольку вектор XY является суммой двух векторов (отступим от предыдущей записи - XY = (5/7) * [a * CX + b * MY] + (2/7) * [a * XM + b * YB]), мы можем сравнить координаты вектора XY с координатами линейной комбинации векторов CX, MY, XM и YB.

Таким образом, мы получим систему уравнений:

(5/7) * a + (2/7) * b = x (координата X вектора XY)
(5/7) * a + (2/7) * b = y (координата Y вектора XY)

Решая эту систему уравнений можно найти значения a и b.

Для лучшего понимания решения, вы могли бы данные использовать конкретные значения координат, например:
CX = (1, 2)
XM = (3, 4)
MY = (-1, -2)
YB = (-3, -4)

Подставится данные значения в выражение выше и решить систему уравнений.