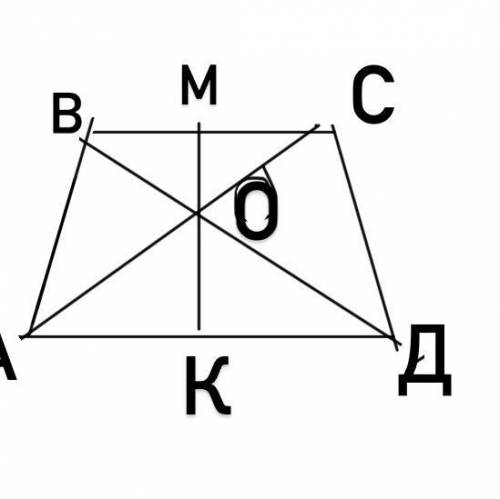
Точка О. Пересечение диагоналей трапеции АВСД. MK-произвольная прямая, проходящая через точку О. И пересекает основания.
Доказать что BМ относится к МС= DK относится к

Объяснение:

Дано:

Трапеция АВСD

прямая FG

Доказать что

Доказательство

АВСD - трапеция => ВС || АD

Тогда диагонали АС, ВD и прямую FG можно рассматривать как секущие при 2х параллельных.

Соответственно,

- будут равны углы (как накрест лежащие):

- будут равны как вертикальные:

Рассм. подобные ∆-ки.

Вследствие равенства углов подобны:

∆АОК и ∆СОМ

∆DОК и ∆BОМ.

Коэффициент подобия:

Oчевидно, что в обоих случаях коэффициент подобия можно выразить через одно и то же соотношение, а значит коэффициенты равны:

Что и требовалось доказать