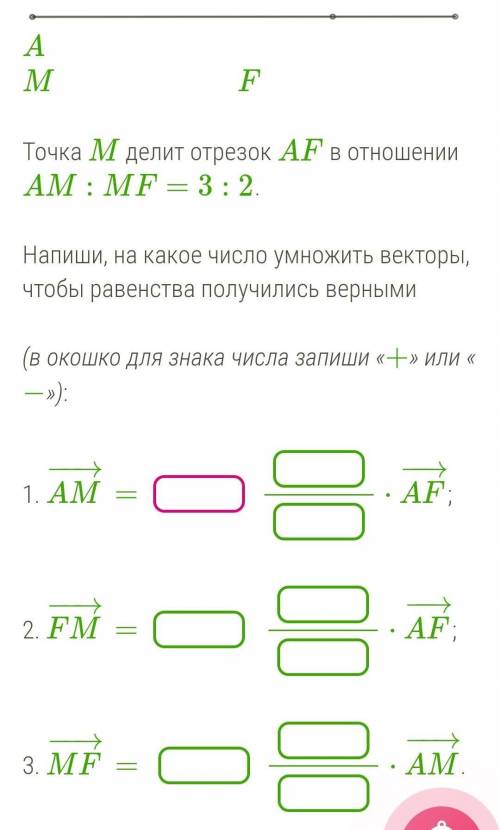
Точка M делит отрезок AF в отношении AM:MF=3:2. Напиши, на какое число умножить векторы, чтобы равенства получились верными (в окошко для знака числа запиши «+» или «−»):
Другие вопросы по теме Геометрия
Популярные вопросы
- [tex] |4x - 3| = 2 \\ |4 - 5x| \\ |9x + 2| - {3}^{2} = ( - {3}^{3}...
2 - Вычислить площадь фигуры, ограниченными линиями y=1/4x^3, x-y=0...
2 - Лабораторная по ,желательно с расчетами , ❤️...
2 - Write the words into the correct order. use full verb forms in...
1 - сакен при покупке книги дал кассиру 500 тенге и получил сдачу 3/25...
3 - Построй график уравнения 3х-3у+6=0. можно с объяснением, а можно...
3 - для того чтобы подчеркнуть хрупкость и недолговечность мечтаний,...
3 - Номер 3. решение с объяснением...
2 - 3)разложите на множители и найдите целые корни многочленаx-3x-4х+12...
3 - Решить у карата было 12 сладостей [tex] \frac{2}{5} [/tex]из них...
2
Пусть векторы AM и MF обозначаются как a и b соответственно.
Мы знаем, что AM:MF=3:2, что означает, что вектор AM составляет 3/5 отрезка AF, а вектор MF занимает 2/5 отрезка AF.
Вектор AF можно представить как сумму векторов AM и MF, то есть AF = a + b.
Теперь, чтобы равенства a = k*(a + b) и b = k*(a + b) были верными, где k - неизвестное число, на которое нужно умножить векторы, чтобы получить равенства, мы можем использовать пропорцию:
AM/MF = a/b = 3/2.
Так как a = (3/5)AF и b = (2/5)AF, подставим эти значения в пропорцию:
[(3/5)AF]/[(2/5)AF] = 3/2.
Упростив выражение, получим:
(3/5)/(2/5) = 3/2.
Мы удаляем AF из обоих частей этой пропорции, так как он встречается и в числителе, и в знаменателе.
Теперь нам нужно найти значение выражения (3/5)/(2/5):
(3/5)/(2/5) = (3/5) * (5/2) = 3/2.
Заметим, что получившееся значение равно значению исходной пропорции AM/MF.
Значит, чтобы равенства a = k*(a + b) и b = k*(a + b) были верными, число k должно быть равно 3/2.
Ответ: На число 3/2 нужно умножить векторы a и b.