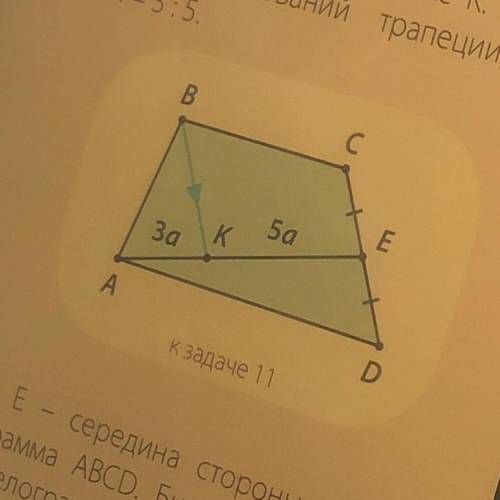
Точка E – середина боковой стороны CD трапеции ABCD. Параллельно этой стороне
через вершину В провели прямую, которая
пересекла отрезок AE в точке К. Найдите
отношение оснований трапеции, если
АК: EK = 3:5.

Добрый день!

Чтобы решить эту задачу, нам понадобятся некоторые свойства трапеции. Сначала рассмотрим отношение сторон трапеции ABCD.

Для начала, обратим внимание, что параллельные стороны трапеции имеют равные меры. Таким образом, сторона AB равна стороне CD.

Также, по свойству, середина отрезка, соединяющего основания трапеции, делит его на две равные части. То есть, отрезок AE равен отрезку EC.

Обозначим m - меру отрезка AE. Тогда, согласно условию задачи, длина отрезка EK равна 3/5 * m, а отрезка KA - 3/5 * m * 3/5.

Теперь мы можем записать условие пропорции, используя полученные равенства:
AK:EK = 3:5
(3/5 * m * 3/5):(3/5 * m) = 3:5
(9/25 * m):(3/5 * m) = 3:5
(9/25)/(3/5) * m/m = 3/5

Заметим, что m сокращаются, и остаемся с пропорцией:
(9/25)/(3/5) = 3/5

Дальше, нам нужно найти отношение оснований трапеции. Обозначим стороны трапеции AB и CD через a и c соответственно. Так как мы знаем, что сторона AB равна стороне CD, мы можем записать:
a/c = 3/5

Таким образом, отношение оснований трапеции равно 3/5.

Надеюсь, это понятно. Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь задавать их!