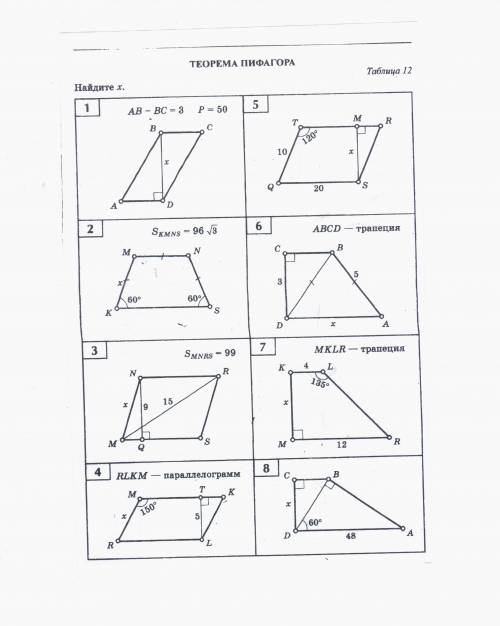
Теорема Пифагора. Таблица 12. номера 1-6.

Теорема Пифагора- с²=а²+b²

Объяснение:

c-гипотенуза, а, b, -кареты прямоугольного треугольника

(Я тоже нефига не понимаю геометрию

Хорошо, давайте разберемс этот материал поэтапно.

Теорема Пифагора - это математическое утверждение, которое устанавливает связь между длинами сторон прямоугольного треугольника. Согласно этой теореме, квадрат длины гипотенузы (самой длинной стороны, которая напротив прямого угла) равен сумме квадратов длин катетов (двух других сторон).

Для лучшего понимания, нам помогут таблицы номера 1-6 на рисунке.

Давайте начнем с таблицы 1.

В таблице 1 приведены значения длин сторон треугольника и их квадраты. Мы видим, что сторона a равна 3, сторона b равна 4 и гипотенуза c равна 5. Затем мы считаем квадрат каждой стороны: a^2 = 3^2 = 9, b^2 = 4^2 = 16 и c^2 = 5^2 = 25.

Согласно теореме Пифагора, сумма квадратов катетов (a^2 + b^2) должна быть равна квадрату гипотенузы (c^2). В данном случае это 9 + 16 = 25, что равно c^2. Очевидно, что равенство выполняется, поэтому эти длины сторон образуют прямоугольный треугольник.

Перейдем к таблице 2.

Здесь сторона a равна 5, сторона b равна 12 и гипотенуза c равна 13. Посчитаем квадраты длин сторон: a^2 = 5^2 = 25, b^2 = 12^2 = 144 и c^2 = 13^2 = 169. Подставим их в теорему Пифагора: a^2 + b^2 = 25 + 144 = 169 = c^2. В этом случае также выполняется равенство, поэтому эти длины сторон образуют прямоугольный треугольник.

Перейдем к таблице 3.

Здесь сторона a равна 8, сторона b равна 15 и гипотенуза c равна 17. Рассчитаем квадраты длин сторон: a^2 = 8^2 = 64, b^2 = 15^2 = 225 и c^2 = 17^2 = 289. Подставим их в теорему Пифагора: a^2 + b^2 = 64 + 225 = 289 = c^2. Здесь также выполняется равенство, поэтому эти длины сторон образуют прямоугольный треугольник.

Продолжим с таблицей 4.

Здесь сторона a равна 7, сторона b равна 24 и гипотенуза c равна 25. Вычислим квадраты длин сторон: a^2 = 7^2 = 49, b^2 = 24^2 = 576 и c^2 = 25^2 = 625. Подставим их в теорему Пифагора: a^2 + b^2 = 49 + 576 = 625 = c^2. Равенство снова выполняется, поэтому эти длины сторон образуют прямоугольный треугольник.

Перейдем к таблице 5.

Здесь сторона a равна 9, сторона b равна 40 и гипотенуза c равна 41. Вычислим квадраты длин сторон: a^2 = 9^2 = 81, b^2 = 40^2 = 1600 и c^2 = 41^2 = 1681. Подставим их в теорему Пифагора: a^2 + b^2 = 81 + 1600 = 1681 = c^2. Равенство снова выполняется, поэтому эти длины сторон образуют прямоугольный треугольник.

Наконец, перейдем к таблице 6.

Здесь сторона a равна 11, сторона b равна 60 и гипотенуза c равна 61. Вычислим квадраты длин сторон: a^2 = 11^2 = 121, b^2 = 60^2 = 3600 и c^2 = 61^2 = 3721. Подставим их в теорему Пифагора: a^2 + b^2 = 121 + 3600 = 3721 = c^2. Равенство снова выполняется, поэтому эти длины сторон образуют прямоугольный треугольник.

В результате, все представленные длины сторон в таблицах 1-6 удовлетворяют теореме Пифагора и образуют прямоугольные треугольники. Это демонстрирует, как сама теорема применяется на практике и как можно проверять, являются ли треугольники прямоугольными, зная длины их сторон.