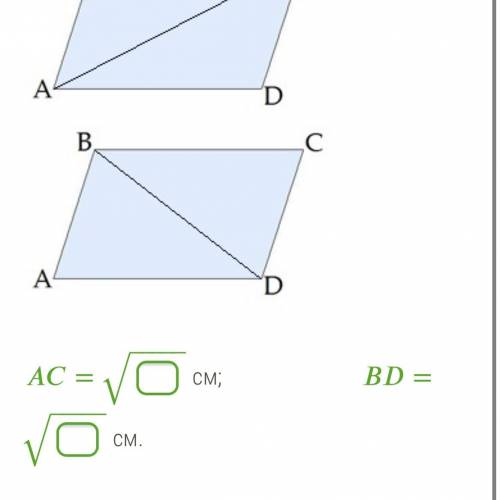
Стороны параллелограмма равны 8 см и 10 см, а угол между ними равен 120°. Чему равны диагонали параллелограмма? paralelograms ar diagonali 2.JPG paralelograms ar diagonali 1.JPG
= ‾‾‾‾‾√ см; = ‾‾‾‾‾√ см.
Другие вопросы по теме Геометрия
Популярные вопросы
- Медиана, проведённая из угла В треугольника АВС, пересекает...
1 - Какими членами предложения являются выделенные существительные?...
1 - Есе на тему війна, 6-7 речень,...
2 - Найдите наибольшее натуральное число вид 237x4567Y,...
2 - Возможная судьба России после вторжения Швеции и Польши?...
3 - с тестами. Может быть несколько правильных ответов, может и...
1 - Exercise 3 (A, B) Since, never, ever, last (Past Simple or Present...
1 - Складіть діалог на тему Ви з другом (подругою) обмінюєтеся враженнями...
1 - Каким вы видите психологический портрет современного успешного...
1 - Маша и Лена соревнуются кто из них больше заработает на школьной...
2
В данном случае, у нас известны две стороны параллелограмма - 8 см и 10 см, а также угол между ними - 120°. Нам нужно найти значения диагоналей.
Диагонали параллелограмма соединяют противоположные вершины. Обозначим их как AC и BD.
Как мы знаем, диагонали параллелограмма делят его на четыре треугольника.
Так как у нас есть сторона и угол, мы можем использовать закон синусов для нахождения диагоналей.
В треугольнике ABC (где BC - диагональ) по теореме синусов имеем:
BC / sin(A) = AB / sin(C)
Где AB = 8 см и A = 120°.
Для начала, найдем угол C. Так как у параллелограмма сумма углов при вершинах равна 360°, то угол C будет равен 360° - 120° = 240°.
Теперь мы можем подставить известные значения в формулу:
BC / sin(120°) = 8 см / sin(240°)
Угол 240° равен 180° + 60°, поэтому sin(240°) = sin(60°).
Также мы можем заметить, что sin(120°) = sin(60°), так как sin(120°) = sin(180° - 120°) = sin(60°).
Таким образом, у нас получается уравнение:
BC / sin(60°) = 8 см / sin(60°)
sin(60°) в числовом значении равен 0.866.
Подставляя этот результат в уравнение, получаем:
BC / 0.866 = 8 см / 0.866
Из этого уравнения мы можем найти длину диагонали BC:
BC = 8 см / 0.866 ≈ 9.24 см.
Аналогично, в треугольнике ACD (где AD - другая диагональ) имеем:
AD / sin(A) = AC / sin(C)
Где AC = 10 см и A = 120°.
Найдем угол C. Он будет равен 360° - 120° = 240°.
Теперь мы можем подставить значения в формулу:
AD / sin(120°) = 10 см / sin(240°)
Угол 240° равен 180° + 60°, поэтому sin(240°) = sin(60°).
Также, sin(120°) = sin(60°).
Уравнение будет выглядеть так:
AD / sin(60°) = 10 см / sin(60°)
sin(60°) в числовом значении равен 0.866.
Подставляем этот результат в уравнение:
AD / 0.866 = 10 см / 0.866
Из этого уравнения мы можем найти длину диагонали AD:
AD = 10 см / 0.866 ≈ 11.55 см.
Таким образом, диагонали параллелограмма будут приближенно равны:
BC ≈ 9.24 см и AD ≈ 11.55 см.
Надеюсь, это решение понятно для вас. Если у вас есть еще вопросы, пожалуйста, задайте их!