Стороны основания прямого параллелепипеда, равны 2 и 3 см, угол между ними 60°, а высота параллелепипеда √6 см. найдите большую диагональ параллелепипеда.​

Объяснение:

Чтобы говорить об одном и том же параллелепипеде, я нарисовал рисунок и прикрепил его, переверните для удобства, а то фото неправильно загрузилось. Итак.

Большой диагональю параллелепипеда называется самая большая его диагональ, которая проходит сквозь всего его, на рисунке таких диагоналей можно построить целых 4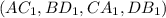 . Они все равны и я буду находить  .

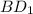Смотрим на него внимательно и видим, что если провести диагональ в основании BD, то получится прямоугольный треугольник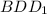 . У нас известен один из его катетов, а надо найти гипотенузу. Найдем катет BD. Он находится в свою очередь в другом прямоугольном треугольнике CBD, где известны оба катета, они равны 2 и 3. По теореме Пифагора:

Теперь применяем теорему Пифагора, чтобы найти диагональ: