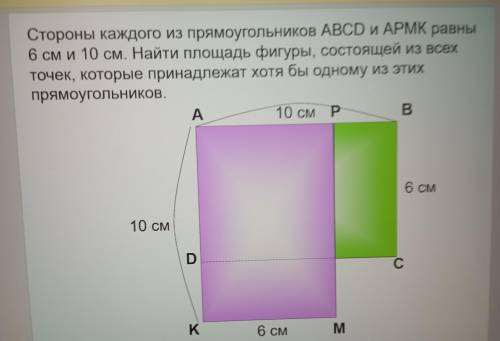
Стороны каждого из прямоугольников ABCD и АРМК равны 6 см и 10 см. Найти площадь фигуры состоящий из всех точек которые принадлежат хотя бы одному из этих прямоугольников

Для решения данной задачи, нам необходимо определить площади прямоугольников ABCD и АРМК, а затем вычислить площадь фигуры, состоящей из всех точек, которые принадлежат хотя бы одному из этих прямоугольников.

1. Начнем с прямоугольника ABCD. У нас известно, что его стороны равны 6 см и 10 см. Площадь прямоугольника можно вычислить по формуле П = а * b, где а - длина, а b - ширина прямоугольника.

Площадь прямоугольника ABCD = 6 см * 10 см = 60 см².

2. Теперь вычислим площадь прямоугольника АРМК. Из условия задачи указано, что его стороны также равны 6 см и 10 см.

Площадь прямоугольника АРМК = 6 см * 10 см = 60 см².

3. Теперь нам нужно найти площадь фигуры, состоящей из всех точек, которые принадлежат хотя бы одному из этих прямоугольников. Для этого нужно найти общую площадь, а затем вычесть площадь, на которой прямоугольники пересекаются.

Чтобы найти общую площадь, мы можем сложить площади обоих прямоугольников:

Общая площадь = Площадь прямоугольника ABCD + Площадь прямоугольника АРМК = 60 см² + 60 см² = 120 см².

Пересечение прямоугольников ABCD и АРМК представляет собой прямоугольник со сторонами, равными 6 см и 6 см. Его площадь равна:

Площадь пересечения = 6 см * 6 см = 36 см².

4. Теперь, чтобы найти площадь фигуры, состоящей из всех точек, которые принадлежат хотя бы одному из этих прямоугольников, нужно вычесть площадь пересечения из общей площади:

Площадь фигуры = Общая площадь - Площадь пересечения = 120 см² - 36 см² = 84 см².

Таким образом, площадь фигуры, состоящей из всех точек, которые принадлежат хотя бы одному из прямоугольников ABCD и АРМК, составляет 84 квадратных сантиметра.