Сторони трикутника дорівнюють 13 см, 14 см і 15 см. Знайдіть висоту трикутника, проведену до його середньої за довжиною сторони.
8 клас
Другие вопросы по теме Геометрия
Популярные вопросы
- Напиши сочинение по картине богатыри План прикреплен...
1 - Основание прямоугольника равно 10м, высота 12м. Из него вырезали квадрат...
1 - 3x-6-2x-1/3объясните как решить подробнее...
3 - 1. Oʻzbekistonda turli xil ini biashi non yetishtiriladi.2. Meva vasabzavotlar...
3 - 1. arccos(1) + 2arcsinus 2. arcctg(1) - п/4...
3 - 2sinA+cosA/3sinA-11cosА= ...
3 - Переписать текст, вставляя пропущенные буквы и знаки препинания. Объяснить...
2 - Кім біледі? өтініш беріңдерші. дәл қазір керек ...
1 - 1. Выпишите глаголы с пропу- щенными буквами. Объясни-те орфограммы.2....
1 - Найти s5 геометрической последовательности b2=3/2 b3=6...
2
12 см
Объяснение:
Стороны треугольника равны 13 см, 14 см и 15 см. Найдите высоту треугольника, проведенную к его средней по длине стороне.
⠀⠀⠀⠀⠀⠀⠀⠀Решение:
Найдем площадь по формуле Герона. Но для начала нужно найти полупериметр этого треугольника , это половина от сумму всех сторон , стороны пусть будут за "а" , "b" , "c" .
Тогда если подставить :
Теперь пора использовать формулу Герона , которая выглядит следущим образом:
Тогда если подставить :
Из другой формулы нахождения площади, которая равна половине от произведения стороны на высоту , но нужно знать , именно та сторона , на которую проведенна высота , а это у нас средняя , которая равна 14 см :
Подставим , тогда из этот формулы найдём высоту (h) :
Решение.
Воспользуемся двумя формулами площади треугольника: формулой Герона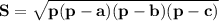 и
и 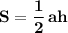 .
.
По условию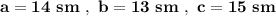 .
.
Сторона со средней длиной - это сторона а=14 см .
Из второй формулы площади выразим высоту h :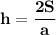 .
.
ответ: h=12 см .
.
АН⊥ВС . Обозначим СН=х , тогда ВН=14-х , h=AH .
ΔАВН: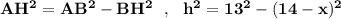
ΔACH: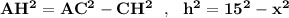
Теперь найдём высоту: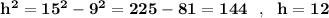 (см)
(см)