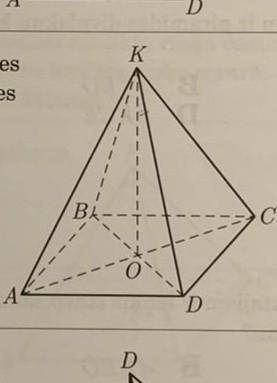
Сторона правильной четырехугольной пирамиды имеет длину 6√2, а противоположные боковые грани перпендикулярны. Диагональное сечение пирамиды равно?
Другие вопросы по теме Геометрия
Популярные вопросы
- Якщо сума двох кутів паралелограма дорівнює 270 градусів, то його менший...
1 - Сор по английскому языку 7 класс 4 четверть ...
2 - Определите цель текста Определите целевую аудиторию текста Определите...
2 - ІВ! ДО ТЬ! ЗАДАЧА, 7 КЛАСкамінь кинули вертикально вгору зі швидкістю...
2 - с задачей Определить нормы естественной убыли колбасы копченой, которая...
2 - Ананын тулгалык ерекшелигин тусиндиретин адеби эссе жазыныз (70-80соз...
1 - Культурні пам ятки України доби бароко (назвати їх)...
2 - Визначіть значення відносної молекулярної маси амінопропанової кислоти...
2 - Формула нахождения (h) с помщью массы и высоты...
1 - Електричний струм в електролітах являє собою напрямлений рух:А) Вільних...
3
ответ: Из точки К на основания двух противоположных боковых граней опустим апофемы КН и КН1. Угол НКН1 = 90 градусов (так как грани перпендикулярны и КН ⊥ AD, КН1 ⊥ BC). Из условия задачи следует, что НН1 = 6√2. Рассмотрим ΔНКН1 - прямоугольный. В нем КН=КН1=НН1/√2=6√2/√2=6. Теперь рассмотрим ΔОКН - тоже прямоугольный, тк КО - высота пирамиды. ОН=1/2 * НН1= 6√2/2=3√2.
По теореме Пифагора: КО² = КН² - ОН² = 6²-18 = 18 ⇒ КО = 3√2.
АС - диагональ квадрата ABCD, она равна DC*√2 = 6√2*√2 = 12.
Площадь ΔКАС(площадь диагонального сечения) = 1/2 * КО * АС =
= 1/2 * 3√2 * 12 = 18√2