Сторона основания правильной треугольной призмы равна 8 см, а диагональ боковой грани равна 10 см. найдите площадь боковой и полной поверхности призмы.

Sбок.= Pосн.*H; Sп.п= Sбок.+2Sосн.

=10^{2}-8^{2}=36, h=6

Pосн.=8*3=24; Sбок.=24*6=144

Sосн=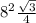=16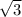

Sп.п=144+32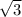

Здравствуйте! Давайте решим эту задачу пошагово.

1) Найдем высоту треугольной призмы. Для этого воспользуемся теоремой Пифагора: квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин катетов.

Гипотенуза треугольника на плоскости — это диагональ боковой грани, поэтому ее длина равна 10 см.
Длина основания — это сторона треугольника, а так как основание правильной треугольной призмы равно 8 см, то каждая сторона треугольника равна 8 см / 2 = 4 см.

Теперь применим теорему Пифагора:
4^2 + Высота^2 = 10^2
16 + Высота^2 = 100
Высота^2 = 100 - 16
Высота^2 = 84.

Из этого мы можем вычислить высоту, взяв квадратный корень из обеих частей:
Высота = √84.

2) Теперь найдем площадь боковой поверхности.

Площадь боковой поверхности призмы можно найти, умножив периметр основания на высоту призмы. У нас основание - правильный треугольник, поэтому его периметр равен 3 * сторона.
Таким образом, площадь боковой поверхности равна 3 * сторона * высота = 3 * 4 см * √84 см ≈ ______ (подставляйте значения в ваш калькулятор и найдите окончательный числовой ответ).

3) Найдем полную поверхность призмы.

Полная поверхность призмы состоит из боковой поверхности и оснований. Основание - это правильный треугольник, а его площадь можно найти с помощью формулы:
Площадь основания = (сторона^2 * √3) / 4.

Таким образом, полная поверхность призмы равна площади боковой поверхности плюс два раза площадь основания:
Полная поверхность = Площадь боковой поверхности + 2 * Площадь основания = _________ (подставляйте значения из предыдущих расчетов и найдите окончательный числовой ответ).

Вот и все! Если у вас есть еще вопросы, я с радостью на них отвечу.