Сторона квадрата равна 12 вычислите длину окружности а) вписанной в квадрат б)описанной около квадрата.
Другие вопросы по теме Геометрия
Популярные вопросы
- Красворд с вопросами и ответами на тему: нового времени...
2 - Эссе на тему: - ключом ко всякой науке является вопросительный знак...
2 - Почему аббревиатура кшт склоняется по падежам ? дайте...
1 - На столе стояла ваза с конфетами. миша съел треть конфет. потом подошёл лёша...
2 - Переведите ,только не через инет the importance of vologda in the 16th century...
2 - Для каких профессий может понадобиться обществознание?...
1 - Визначте жорсткість пружини, якщо під дією сили 6 н вона подовжилася на 2 см....
2 - M=4.9 10^{24} kg r= 6100 kg g-? [/tex]...
2 - Сделай синтаксический разбор предложения.. когда зацвела ива,полетели гости...
3 - Почему пустыня намыб образовалась на узбережжы атлантического...
3
Дано: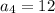
Длина окружности ровна: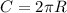
Мы знаем, что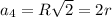 , где
, где 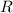 - радиус описанной окружности, а
- радиус описанной окружности, а  - вписанной
- вписанной