1. Геометрия
  2. Срешением , ! ❤❤❤ доказать

Срешением , ! ❤❤❤
доказать ,что векторы a b c образуют базис, и найти координаты вектора d в этом базисе.

maxprok2012 maxprok2012    3   22.09.2019 20:51    1

Ответы
Weltrаum Weltrаum  10.09.2020 14:36

\left(\begin{array}{ccc}-2&3&4\\ 5&2&-3\\ 1&-7&2\end{array}\right|\left\begin{array}{ccc}-4\\22\\-13\end{array}\right)^{I:(-2)}\sim\left(\begin{array}{ccc}1&-1.5&-2\\ 5&2&-3\\ 1&-7&2\end{array}\right|\left\begin{array}{ccc}2\\22\\-13\end{array}\right)^{II-5I}_{III-I}\sim\\ \\ \\ \sim\left(\begin{array}{ccc}1&-1.5&-2\\ 0&9.5&7\\ 0&-5.5&4\end{array}\right|\left\begin{array}{ccc}2\\12\\-15\end{array}\right)^{II:9.5}\sim\left(\begin{array}{ccc}1&-1.5&-2\\ 0&1&\frac{14}{19}\\ 0&-5.5&4\end{array}\right|\left\begin{array}{ccc}2\\\frac{24}{19}\\-15\end{array}\right)^{I+1.5II}_{III+5.5II}\sim

\sim\left(\begin{array}{ccc}1&0&-\frac{17}{19}\\ 0&1&\frac{14}{19}\\ 0&0&\frac{153}{19}\end{array}\right|\left\begin{array}{ccc}\frac{74}{19}\\ \frac{24}{19}\\ -\frac{153}{19}\end{array}\right)\sim\left(\begin{array}{ccc}1&0&-\frac{17}{19}\\ 0&1&\frac{14}{19}\\ 0&0&1\end{array}\right|\left\begin{array}{ccc}\frac{74}{19}\\ \frac{24}{19}\\ -1\end{array}\right)^{I+\frac{17}{19}III}_{II-\frac{14}{19}III}\sim\\ \\ \\ \sim\left(\begin{array}{ccc}1&0&0\\0&1&0\\ 0&0&1\end{array}\right|\left\begin{array}{ccc}3\\2\\-1\end{array}\right)

Данная система векторов образует базис (линейно независимая система векторов), так как все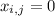 x_{i,j}=0, i\ne j

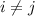
Разложение вектора по базису:

\overline{d}=3\overline{a}+2\overline{b}-\overline{c}=\{3;2;-1\}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
icon21 icon21  10.09.2020 06:25
43. а) Әрбір бұрышы: 1) 60°; 2) 90° болатын дөңес көпбұрыштың неше қабырғасы бар?ә) Егер ZA = ZC= 60°, ал ZB = 1,4 - 2D болса, ABCD дөңес төрт-бұрышының В және D бұрыштарын...
kassssseta kassssseta  10.09.2020 06:26
Найдите площадь прямоугольного треугольника если гипотенуза равна 20 один из катетов 10 противолежаший ему угол равен 30°...
Yourstudentbook Yourstudentbook  09.09.2020 06:22
В треугольнике abc ab=bc медиана bm = 6. S = 12√7. найдите ab​...
makovskaya2001 makovskaya2001  10.09.2020 06:47
Сумма внутренних и сумма внешних углов выпуклого многоугольника Установи соответствие между сторонами правильного многоугольника и внешними углами правильного многоугольника....
brilovainna brilovainna  14.09.2019 15:00
Решить вот дано: прямоугольная трапеция abcd высота из вершины c, угол с равен 120 градусов...
Obsharovak Obsharovak  14.09.2019 15:00
Найдите координаты вершины в параллелограмма abcd если а(3; -2) с(9; 8) d(-4; -5)...
ляляляляляляля1 ляляляляляляля1  14.09.2019 15:00
Подобны ли треугольники авс и def, если в этих треугольниках ас=44см, ав=52см,вс=76см,de=15,6 см,df=22cм,ef=13,2см...
annkhanenko23 annkhanenko23  14.09.2019 15:00
Впрямоугольном треугольнике катет лежащий против угла в 60 градусов равен 5 корней из 3. найдите другие стороны треугольника и площадь ! подробно,...
Alexal16 Alexal16  28.10.2020 15:09
СДЕЛАЙТЕ ГЕОМЕТРИЮ ВСЕ ЗАДАНИЕ УВАЖЕНИЕ...
gimnastikgirla gimnastikgirla  28.10.2020 15:11
2. Точка M лежит на стороне ВС паралелограмма ABCD, причем BM MC =3:1. Вырату пектор AM через некторы BC =a BA=b​...

Популярные вопросы