Составить каноническое уравнение эллипса
А(-3:0) B(1;√40/3)
Другие вопросы по теме Геометрия
Популярные вопросы
- Решите уравнение 2+ x+17/5=3x-7/4 p.s. x+17/5, 3x-7/4 это дроби...
1 - Нужно подобрать фразеологизм со значением не нужен...
1 - Укажите (с стрелочек в структурных формулах) смещение электронных пар в молекулах...
1 - Два маленьких вопроса из перечисленного относится к прирожденному статусу?...
2 - Многим животным человек поставил памятники.что ты об этом знаешь? какому животному...
3 - Составить предложение из слов. 1. сказки прелесть что за эти 2. там царевна...
3 - Дано трапеция авсд угола=36градусов уголс =117 г8радусов найти углы в и д...
1 - Вкружке юных иллюзионистов 18 мальчиков, что в 2 раза больше, чем девочек....
2 - Надо написать 10 словосочетаний с словарными словами на тему интерьер...
2 - От скрещивания растений дурман с колючими коробочками между собой,получено...
2
Объяснение:
Каноническое уравнение имеет вид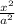 +
+ 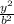
Решим систему уравнений
Пусть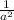 = U и
= U и  =V, тогда 9u=1 u=1/9
=V, тогда 9u=1 u=1/9
u+(40/9)v=1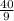 v=
v=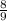
Уравнение принимает вид +
+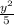 =1
=1