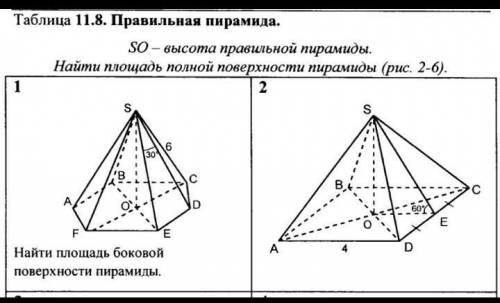
SO -высота правильной Пирамиды
Найти площадь боковой поверхности пирамиды.
​

Площадь боковой поверхности пирамиды можно найти по формуле: П = (периметр основания) х (полувысота боковой грани).

Для решения задачи нам нужно знать и площадь основания пирамиды, и высоту боковой грани пирамиды.

На основании данного изображения можно видеть, что основанием этой пирамиды является правильный пятиугольник. Правильный пятиугольник - это пятиугольник, у которого все стороны равны, а все углы равны между собой. Чтобы найти площадь основания пирамиды, нужно знать длину одной стороны пятиугольника.

Так как пятиугольник является правильным, его можно разделить на 5 равных треугольников, при этом центральный угол каждого треугольника будет равняться 360 градусов / 5 = 72 градусам. Каждый треугольник будет равнобедренным, так как у него две стороны и два угла будут равны.

Чтобы узнать длину одной стороны пятиугольника, нужно разделить его на два прямоугольных треугольника внутри пирамиды. Каждый из этих треугольников будет прямоугольным с гипотенузой, равной длине стороны правильного пятиугольника.

Зная эти детали, можно продолжить расчеты. Так как SO - это высота пирамиды, она будет равна одной из боковых сторон внутреннего треугольника. Для удобства будем называть эту сторону а.

Полувысота боковой грани пирамиды будет равна длине высоты минус радиус окружности. Радиус окружности можно найти, зная, что это половина длины стороны пирамиды в основании.

Итак, начнем с вычисления длины стороны пятиугольника. Если мы разделим пятиугольник на два прямоугольных треугольника, каждый угол прямоугольного треугольника будет равен 72 градусам, а его гипотенуза будет равняться длине стороны пятиугольника. Мы можем использовать тригонометрическую формулу для нахождения длины гипотенузы:

а = 2R sin(36°)

Где R - это радиус окружности, вписанной в пятиугольник. Радиус окружности можно найти, зная, что это половина длины стороны пятиугольника:

а = 2 (R/2) sin(36°)
а = R sin(36°)

Теперь мы можем перейти к расчету полувысоты боковой грани пирамиды. Полувысота будет равна длине SO минус радиус окружности:

полувысота = SO - R

Теперь имея полувысоту и длину стороны, мы можем найти площадь боковой поверхности пирамиды:

П = (периметр основания) х (полувысота боковой грани)
П = 5а × (полувысота)

Надеюсь, эта информация окажется полезной для вашего решения задачи. Если у вас возникнут дополнительные вопросы, не стесняйтесь задавать.