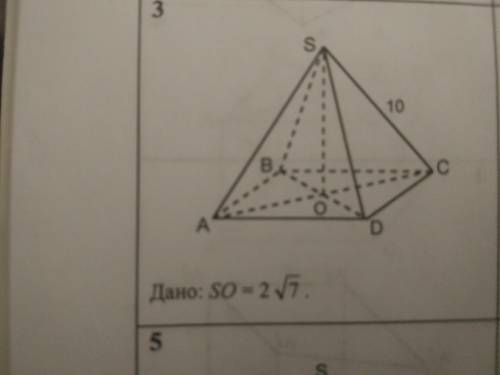
SO-высота правильной пирамиды. Найти площадь полной поверхности пирамиды.
Другие вопросы по теме Геометрия
Популярные вопросы
- Плюсы правления сталина и аргументы ...
3 - Постройте треугольник mnk если угол м=45 градусов мк=6 см кn=7 см...
2 - 1.укажите точку,принадлежащую прямой,заданной уравнением 3х+y-1=0 а(1;...
1 - Найдите первый положительный член арифметической прогрессии: -35,-27, -19,...
2 - Сумма четных и нечетных чисел от 1 до 1000 включительно...
1 - От пристани одновременно в одном направление отошли теплоход со скоростью...
2 - Решить номер тема теорема виета ...
3 - Знайдіть кількість сторін правильного многокутника центральний кут якого...
3 - Как найти изменение потенциальной энергии ? ...
3 - Согласны ли вы с утверждением что характер определяет судьбу человека...
3
1. Начнем с основания пирамиды, которое в этой задаче является правильным шестиугольником. Правильный шестиугольник имеет все стороны одинаковой длины (в нашем случае, все стороны равны SO), и все углы равны 120 градусам. Для расчета площади этого шестиугольника, нам понадобится знать его формулу.
Формула для расчета площади правильного шестиугольника: Площадь = (3 * квадратный корень из 3 * сторона^2) / 2.
В нашем случае, площадь основания пирамиды будет:
Площадь основания = (3 * √3 * SO^2) / 2.
2. Теперь нас интересует площадь боковых граней пирамиды. В нашем случае, пирамида имеет 4 боковые грани, и они являются равносторонними треугольниками. Равносторонний треугольник имеет все стороны одинаковой длины (в нашем случае, все стороны равны SO), и все углы равны 60 градусам.
Формула для расчета площади равностороннего треугольника: Площадь = (квадратный корень из 3 * сторона^2) / 4.
Так как у нас 4 боковые грани, то площадь всех боковых граней пирамиды будет:
Площадь боковых граней = 4 * (квадратный корень из 3 * SO^2) / 4.
3. Теперь, чтобы найти площадь полной поверхности пирамиды, нужно сложить площади основания и всех боковых граней:
Площадь полной поверхности = Площадь основания + Площадь боковых граней.
Подставляем значения из пунктов 1 и 2:
Площадь полной поверхности = (3 * √3 * SO^2) / 2 + 4 * (квадратный корень из 3 * SO^2) / 4.
Подводя итог, площадь полной поверхности пирамиды можно найти, используя формулу:
Площадь полной поверхности = (3 * √3 * SO^2) / 2 + 4 * (квадратный корень из 3 * SO^2) / 4.
Таким образом, с помощью данной формулы и подставив значение SO, можно рассчитать площадь полной поверхности пирамиды.