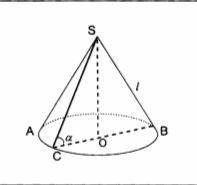
SO – высота конуса. Найти объем и площадь боковой поверхности конуса.

V = 1/3 πR²H

V = 1/3 π (CO)² SO

S = πRl

S = π CO CS

Для решения данной задачи нам понадобятся формулы для расчета объема и площади боковой поверхности конуса.

1. Объем конуса:
Объем конуса можно найти с помощью следующей формулы:
V = (1/3) * π * r^2 * h,
где V - объем конуса, π - математическая константа, приблизительно равная 3.14159,
r - радиус основания конуса,
h - высота конуса.

В задаче нам дана высота конуса SO, но радиус основания не указан. Чтобы найти его, нам понадобятся данные о диаметре основания.

2. Нахождение радиуса основания:
В задаче не указан радиус основания конуса, но мы можем вычислить его, зная диаметр основания.
Радиус (r) - это половина диаметра (d), поэтому, чтобы найти радиус, нам необходимо разделить значение диаметра на 2.

3. Нахождение диаметра основания:
На чертеже, данном в задаче, нам дана горизонтальная линия AB, которую мы можем считать диаметром, так как она проходит через центр основания конуса. Поэтому диаметр длиной AB будет равен d.

4. Нахождение высоты конуса:
На чертеже, данном в задаче, нам дана вертикальная линия SO, которая символизирует высоту конуса. Это значение имеет обозначение "SO" и дано на чертеже.

Теперь, когда мы получили все необходимые данные, мы можем приступить к расчетам.

Шаги по решению задачи:
1. Найти диаметр основания конуса, измерив горизонтальную линию AB на чертеже. Обозначим его как d.
2. Разделить значение диаметра на 2, чтобы найти радиус основания конуса. Обозначим его как r. То есть r = d/2.
3. Найти объем конуса, используя формулу V = (1/3) * π * r^2 * h. Подставить значения радиуса и высоты в формулу и рассчитать объем.
4. Найти площадь боковой поверхности конуса. Площадь боковой поверхности представляет собой боковую поверхность, которая не включает в себя площади основания конуса.
Для подсчета площади боковой поверхности можно использовать формулу S = π * r * l, где S - площадь боковой поверхности, r - радиус основания, l - образующая конуса.
Образующую конуса можно найти, используя теорему Пифагора для нахождения гипотенузы. Применим формулу известных сторон: l = sqrt(h^2 + r^2).
Подставим значения радиуса и высоты в формулу и рассчитаем площадь боковой поверхности конуса.

Таким образом, мы рассчитали объем и площадь боковой поверхности конуса с помощью предложенных шагов и соответствующих формул. Все значения были обоснованы и проиллюстрированы на чертеже.