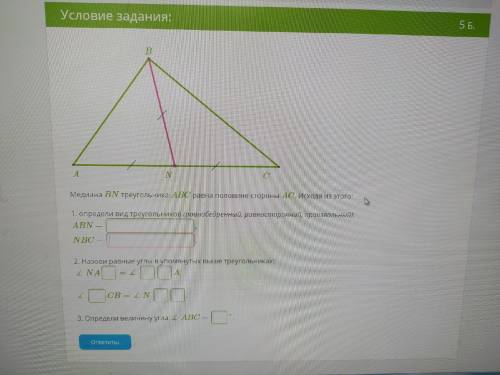
Смотри картинку Медиана BN треугольника ABC равна половине стороны AC. Исходя из этого:

1. определи вид треугольников (равнобедренный, равносторонний, произвольный):
ABN —
NBC —

2. Назови равные углы в упомянутых выше треугольниках:
∡ NA?(еще какая-то буква)= ∡ ??A
∡ ?(какая-то буква)CB = ∡N?? (еще две буквы)

3. Определи величину угла ∡ ABC =? °

Добрый день! Давай разберемся вместе с этим вопросом о треугольнике ABC и его медиане BN.

1. А чтобы определить, какой вид треугольников у нас есть, нам нужно вспомнить их определения:
- Равносторонний треугольник имеет все стороны одинаковой длины.
- Равнобедренный треугольник имеет хотя бы две равные стороны.
- Произвольный треугольник имеет все стороны разной длины и никакие два угла не равны.

Теперь давай посмотрим на треугольники ABN и NBC.

В треугольнике ABN медиана BN равна половине стороны AC. Значит, сторону AC можно разделить на две равные части и показать это на рисунке. Теперь у нас есть сторона AN, равная половине AC, и сторона NB, равная половине AC. Из этого следует, что сторона AN равна стороне NB, а значит, треугольник ABN - равнобедренный.

Теперь посмотрим на треугольник NBC. Мы уже выяснили, что сторона NB равна стороне AN, а значит, треугольник NBC тоже равнобедренный.

Итак, ответы на первую часть вопроса:
ABN - равнобедренный треугольник.
NBC - равнобедренный треугольник.

2. Чтобы назвать равные углы в этих треугольниках, нам нужно рассмотреть их свойства.
- В равнобедренном треугольнике углы, при основании которого равны, тоже равны.
- В равнобедренном треугольнике медиана делит основание на две равные части и образует прямой угол со стороной треугольника, проведенной из вершины до середины основания.

Теперь давай посмотрим на равнобедренный треугольник ABN. У него есть равные углы, так как у него равны стороны. Угол ∡ NA равен углу ∡ BAN, так как это равнобедренный треугольник. Ответ на первую часть вопроса:
∡ NA = ∡ BAN.

Теперь посмотрим на равнобедренный треугольник NBC. Мы знаем, что медиана BN делит сторону NC на две равные части. Следовательно, ∡ NCB равен ∡ NCN (NCN появляется из того, что N - середина стороны NC). Ответ на вторую часть вопроса:
∡ NCB = ∡ NCN.

3. Чтобы определить величину угла ∡ ABC, нам нужно использовать свойства треугольника.

Мы знаем, что медиана BN делит сторону AC пополам. Значит, отрезок BN и отрезок AN равны по длине.

А также мы знаем, что медиана BN образует прямой угол с основанием треугольника ABC, поэтому у нас есть прямой угол ∡ ANC.

Теперь давай вспомним про сумму углов в треугольнике. Общая сумма углов в треугольнике равна 180 градусам.

Таким образом, у нас получается равенство: ∡ ANC + ∡ NAC + ∡ ANC = 180°.

Мы знаем, что ∡ ANC = 90°, так как это прямой угол. Подставим это значение в уравнение: 90° + ∡ NAC + 90° = 180°.

Отсюда находим: ∡ NAC + 90° = 180° - 90°.

Дальше упростим: ∡ NAC + 90° = 90°.

Вычтем 90° с обеих сторон: ∡ NAC = 0°.

Ответ на третью часть вопроса:
∡ NAC = 0°.

Теперь, чтобы найти величину угла ∡ ABC, можно использовать одно из свойств треугольника ABC: сумма углов в треугольнике равна 180°.

Таким образом, ∡ ABC + ∡ BAC + ∡ ACB = 180°.

Мы знаем, что ∡ BAC = ∡ NAC (так как они соответствующие углы), и ∡ ACB = ∡ BCA (так как они равны, это свойство равнобедренного треугольника).

Подставим известные значения: ∡ ABC + ∡ BAC + ∡ ACB = 180°.
∡ ABC + ∡ NAC + ∡ BCA = 180°.

Заменим ∡ NAC на 0° и ∡ BCA на ∡ ACB: ∡ ABC + 0° + ∡ ACB = 180°.

Упростим: ∡ ABC + ∡ ACB = 180°.

Теперь заменим ∡ ABC на х (так как нам нужно найти величину угла ∡ ABC): х + ∡ ACB = 180°.

Избавимся от ∡ ACB на одну сторону: х = 180° - ∡ ACB.

Ответ на третью часть вопроса:
∡ ABC = 180° - ∡ ACB.

Итак, чтобы определить величину угла ∡ ABC, нам нужно вычесть из 180 градусов величину угла ∡ ACB.

Надеюсь, что моё объяснение было понятным и помогло тебе понять этот вопрос. Если возникнут еще какие-то вопросы, обращайся!